题目内容
10.某市公租房的房源位于A,B,C,D四个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,在该市的甲、乙、丙三位申请人中:(1)求恰有1人申请A片区房源的概率;
(2)用x表示选择A片区的人数,求x的分布列和数学期望.
分析 (1)求出实验发生包含的事件是3位申请人中,满足条件的所有事件有43种结果.恰有1人申请A片区房源结果,然后求解概率.
(2)ξ的所有可能结果为0,1,2,3,求出概率,得到X的分布列然后求解期望即可.
解答 解:(1)本题是一个等可能事件的概率,实验发生包含的事件是3位申请人中,
每一个有四种选择,共有43种结果.
满足条件的事件恰有1人申请A片区房源有$C_3^1•{3^2}$,
根据等可能事件的概率$p=\frac{{c_3^1{3^2}}}{4^3}=\frac{27}{64}$.
(2)ξ的所有可能结果为0,1,2,3,依题意,$p({ξ=0})=\frac{3^3}{4^3}=\frac{27}{64}$,$p({ξ=1})=\frac{{c_3^1•{3^2}}}{4^3}=\frac{27}{64}$,$p({ξ=2})=\frac{c_3^2•3}{4^3}=\frac{9}{64}$,$p({ξ=3})=\frac{1}{4^3}=\frac{1}{64}$,
∴X的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{27}{64}$ | $\frac{27}{64}$ | $\frac{9}{64}$ | $\frac{1}{64}$ |
法2:每个片区被申请的概率均为$\frac{1}{4}$,没被选中的概率均为$\frac{3}{4}$,ξ的所有可能结果为0,1,2,3,
且ξ~B(3,$\frac{1}{4}$),$p({ξ=0})={({\frac{3}{4}})^3}=\frac{27}{64}$,$p({ξ=1})=C_3^1•\frac{1}{4}•{({\frac{3}{4}})^2}=\frac{27}{64}$,$p({ξ=2})=C_3^2•{({\frac{1}{4}})^2}•\frac{3}{4}=\frac{9}{64}$,$p({ξ=3})={({\frac{1}{4}})^3}=\frac{1}{64}$,
∴X的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{27}{64}$ | $\frac{27}{64}$ | $\frac{9}{64}$ | $\frac{1}{64}$ |
点评 本题考查概率的求法,二项分布的分布列以及期望的求法,考查转化思想以及计算能力.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
15.已知集合M={x|x≥-1},N={x|-2<x<2},则M∩N=( )
| A. | (-∞,-1] | B. | [-1,2) | C. | (-1,2] | D. | (2,+∞) |
19.一个几何体的三视图如图所示,则其体积为( )


| A. | π+2 | B. | 2π+4 | C. | π+4 | D. | 2π+2 |
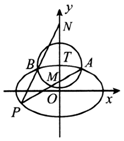 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,以椭圆C的上顶点T为圆心作圆T:x2+(y-1)2=r2(r>0),圆T与椭圆C在第一象限交于点A,在第二象限交于点B.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,以椭圆C的上顶点T为圆心作圆T:x2+(y-1)2=r2(r>0),圆T与椭圆C在第一象限交于点A,在第二象限交于点B.