题目内容
16.若$f(x)=\left\{\begin{array}{l}{3^x},x≤0\\ \frac{1}{x},x>0\end{array}\right.$,则f(f(-2))=9.分析 先求出f(-2)=3-2=$\frac{1}{9}$,从而f(f(-2))=f($\frac{1}{9}$),由此能求出函数值.
解答 解:∵$f(x)=\left\{\begin{array}{l}{3^x},x≤0\\ \frac{1}{x},x>0\end{array}\right.$,
∴f(-2)=3-2=$\frac{1}{9}$,
∴f(f(-2))=f($\frac{1}{9}$)=$\frac{1}{\frac{1}{9}}$=9.
故答案为:9.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
7.已知函数y=f(x)是定义在R上的偶函数,且在(-∞,0]上是增函数,若不等式f(a)≥f(x)对任意x∈[1,2]恒成立,则实数a的取值范围是( )
| A. | (-∞,1] | B. | [-1,1] | C. | (-∞,2] | D. | [-2,2] |
4.若函数$f(x)=\sqrt{3}sin(2x+φ)+cos(2x+φ)(|φ|<\frac{π}{2})$为偶函数,则( )
| A. | f(x)的最小正周期为π,且在$(0,\frac{π}{2})$上为增函数 | |
| B. | f(x)的最小正周期为$\frac{π}{2}$,且在$(0,\frac{π}{4})$上为增函数 | |
| C. | f(x)的最小正周期为$\frac{π}{2}$,且在$(0,\frac{π}{4})$上为减函数 | |
| D. | f(x)的最小正周期为π,且在$(0,\frac{π}{2})$上为减函数 |
8.某企业节能降耗技术改造后,在生产某产品过程中的产量x(吨)与相应的生产能耗y(吨)的几组对应数据如表所示:
若根据表中数据得出y关于x的线性回归方程为y=0.7x+a,若生产7吨产品,预计相应的生产能耗为( )吨.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A. | 5.25 | B. | 5.15 | C. | 5.5 | D. | 9.5 |
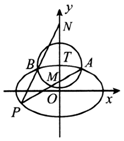 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,以椭圆C的上顶点T为圆心作圆T:x2+(y-1)2=r2(r>0),圆T与椭圆C在第一象限交于点A,在第二象限交于点B.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,以椭圆C的上顶点T为圆心作圆T:x2+(y-1)2=r2(r>0),圆T与椭圆C在第一象限交于点A,在第二象限交于点B.