题目内容
15.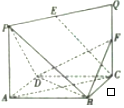 如图,ACQP所在的平面与菱形ABCD所在的平面相互垂直,交线为AC,若$AC=\sqrt{2}AP,E,F$分别是PQ,CQ的中点.求证:
如图,ACQP所在的平面与菱形ABCD所在的平面相互垂直,交线为AC,若$AC=\sqrt{2}AP,E,F$分别是PQ,CQ的中点.求证:(1)CE∥平面PBD;
(2)平面FBD⊥平面PBD.
分析 (1)设AC∩BD=O,连接PO,证明四边形POCE是平行四边形,可得CE∥PO,即可证明CE∥平面PBD;
(2)证明PO⊥平面FBD,即可证明平面FBD⊥平面PBD.
解答  证明:(1)设AC∩BD=O,连接PO,则
证明:(1)设AC∩BD=O,连接PO,则
∵O是AC的中点,E是PQ的中点,
∴PE=OC,PE∥OC,
∴四边形POCE是平行四边形,
∴CE∥PO,
∵CE?平面PBD,PO?平面PBD,
∴CE∥平面PBD;
(2)∵平面ACQP⊥平面ABCD,平面ACQP∩平面ABCD=AC,BD⊥AC,
∴BD⊥平面ACQP,
∵PO?平面ACQP,∴BD⊥PO,
连接AQ,OF,则由三角形相似可AQ⊥PO,
∵F是CQ中点,O是AC的中点,
∴OF∥AQ,
∴OF⊥PO,
∵BD∩OF=O,
∴PO⊥平面FBD,
∵PO?平面PBD,
∴平面FBD⊥平面PBD.
点评 本题是中档题,考查直线与平面平行、垂直,平面与平面垂直的证明的方法,考查空间想象能力,基本知识的灵活运用能力.

练习册系列答案
相关题目
7.已知函数y=f(x)是定义在R上的偶函数,且在(-∞,0]上是增函数,若不等式f(a)≥f(x)对任意x∈[1,2]恒成立,则实数a的取值范围是( )
| A. | (-∞,1] | B. | [-1,1] | C. | (-∞,2] | D. | [-2,2] |
4.若函数$f(x)=\sqrt{3}sin(2x+φ)+cos(2x+φ)(|φ|<\frac{π}{2})$为偶函数,则( )
| A. | f(x)的最小正周期为π,且在$(0,\frac{π}{2})$上为增函数 | |
| B. | f(x)的最小正周期为$\frac{π}{2}$,且在$(0,\frac{π}{4})$上为增函数 | |
| C. | f(x)的最小正周期为$\frac{π}{2}$,且在$(0,\frac{π}{4})$上为减函数 | |
| D. | f(x)的最小正周期为π,且在$(0,\frac{π}{2})$上为减函数 |