题目内容
20.复数z满足$\overline{z}$(1-i)=|1+i|,则复数z的实部与虚部之和为( )| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | 1 | D. | 0 |
分析 利用复数的运算法则、共轭复数的定义、实部与虚部的定义即可得出.
解答 解:∵$\overline{z}$(1-i)=|1+i|,∴$\overline{z}$(1-i)(1+i)=$\sqrt{2}$(1+i),∴$\overline{z}$=$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{2}}{2}$i
∴z=$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{2}$i
则复数z的实部与虚部之和=$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{2}$=0.
故选:D.
点评 本题考查了复数的运算法则、共轭复数的定义、实部与虚部的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
8.某企业节能降耗技术改造后,在生产某产品过程中的产量x(吨)与相应的生产能耗y(吨)的几组对应数据如表所示:
若根据表中数据得出y关于x的线性回归方程为y=0.7x+a,若生产7吨产品,预计相应的生产能耗为( )吨.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A. | 5.25 | B. | 5.15 | C. | 5.5 | D. | 9.5 |
10.掷一枚均匀的硬币3次,出现正面向上的次数恰好为两次的概率为( )
| A. | $\frac{3}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{5}{8}$ | D. | $\frac{1}{2}$ |
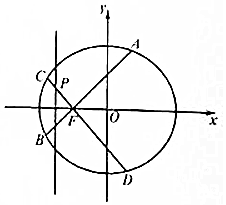 如图,已知F为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左焦点,过点F且互相垂直的两条直线分别交椭圆于A、B及C、D.
如图,已知F为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左焦点,过点F且互相垂直的两条直线分别交椭圆于A、B及C、D.