Question

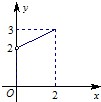已知函数f（x）是定义在[-2，0）∪（0，2]上的奇函数，当x＞0时，f（x）的图象如图所示．
（1）求x∈（0，2]时，f（x）的解析式；
（2）求x∈[-2，0）∪（0，2]时，f（x）的解析式．

Answer 1

考点：函数奇偶性的性质,函数解析式的求解及常用方法

专题：函数的性质及应用

分析：（1）根据图象得直线过点（2，3），（0，2），再由点斜式方程求出直线方程，即可求出∈[-1，0]上的解析式；
（2）设x∈[-2，0），则-x∈（0，2]，根据奇函数的性质求出对应的解析式，再用分段函数求出f（x）在定义域上的解析式．

解答： 解：（1）由图象知：当x∈（0，2]时，函数图象所在直线过点（2，3），（0，2），
其方程为y-2=

1

2

x，即y=

1

2

x+2，
所以当x∈（0，2]时，函数的解析式为f（x）=

1

2

x+2，
（2）设x∈[-2，0）时，-x∈（0，2]，则f（-x）=-

1

2

x+2，
又f（x）是定义在[-2，0）∪（0，2]上的奇函数，
所以当x∈[-2，0）时，f（x）=-f（-x）=

1

2

x-2，
所以f（x）=

1 2 x+2，x∈(0，2] 1 2 x-2，x∈[-2，0)

．

点评：本题考查了函数的奇偶性及其应用，函数解析式的求解，以及数形结合思想，属基础题．