题目内容
两封不同的信，投入3个不同的信箱，则共有 种不同的方法．
考点：计数原理的应用
专题：排列组合
分析：依题意，第一封也有3种投法，第二封也有3种投法，利用分步计数原理可得答案．
解答：
解：两封不同的信，投入3个不同的信箱，
第一封可投入3个不同的信箱中的任意一个，有3种投法，
同理可得，第二封也有3种投法，
由分步计数原理可得，共有3×3=9种投法，
故答案为：9．
第一封可投入3个不同的信箱中的任意一个，有3种投法，
同理可得，第二封也有3种投法，
由分步计数原理可得，共有3×3=9种投法，
故答案为：9．
点评：本题考查计数原理的应用，熟练掌握分步计数原理是解决问题的关键，属于基础题．
练习册系列答案
金状元绩优好卷系列答案
相关题目
若集合A=[-1，1]，B={y|y=x2，x∈R}，则A∩B=（ ）
| A、{x|-1≤x≤1} |
| B、{x|x≥0} |
| C、{x|0≤x≤1} |
| D、∅ |
下列函数中与函数y=x是相同函数的是（ ）
A、y=(
| |||
B、y=
| |||
C、y=
| |||
D、y=
|
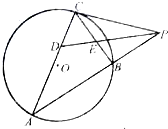如图，PC是圆O的切线，切点为C，直线PA与圆O交于两点A、B，∠APC的平分线分别交弦CA、CB于两点D、E，已知PC=3，PB=2，则等比数列{an}中，S2=7，S6=91，则S4=（ ）
| A、28或-21 | B、28 |
| C、-21 | D、以上都不对 |