题目内容
已知f（x）=
•
-1，其中向量
=（
sin2x，cosx），
=（1，2cosx）（x∈R）．
（Ⅰ）求f（x）的单调递减区间；
（Ⅱ）在△ABC中，角A、B、C的对边分别为a、b、c，f（A）=2，a=
，b=
，求边长c的值．
| a |
| b |
| a |
| 3 |
| b |
（Ⅰ）求f（x）的单调递减区间；
（Ⅱ）在△ABC中，角A、B、C的对边分别为a、b、c，f（A）=2，a=
| 7 |
| 3 |
考点：平面向量数量积的运算,正弦定理,余弦定理
专题：计算题,三角函数的图像与性质,解三角形,平面向量及应用
分析：（Ⅰ）运用向量的数量积的坐标表示，及二倍角的余弦公式和两角和的正弦公式，结合正弦函数的单调减区间，解不等式即可得到所求减区间；
（Ⅱ）由f（A）=2，求出A，再由余弦定理，即可得到c．
（Ⅱ）由f（A）=2，求出A，再由余弦定理，即可得到c．
解答：
解：（Ⅰ）f （x）=
•
-1=（
sin2x，cosx）•（1，2cosx）-1
=
sin2x+2cos2x-1=
sin2x+cos2x
=2sin（2x+
），
由2kπ+
≤2x+
≤2kπ+
，得kπ+
≤x≤kπ+
，
∴f （x）的递减区间为[kπ+
，kπ+
]，（k∈Z）；
（Ⅱ）f（A）=2sin（2A+
）=2，∴sin（2A+
）=1，
由于0＜A＜π，则
＜2A+
＜
，即有2A+
=
，
则有A=
；
由余弦定理得 a2=b2+c2-2bccosA
7=3+c2-3c 即 c2-3c-4=0，即（c-4）（c+1）=0，
解得c=4或c=-1 （不合题意，舍去）
则c=4．
| a |
| b |
| 3 |
=
| 3 |
| 3 |
=2sin（2x+
| π |
| 6 |
由2kπ+
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
∴f （x）的递减区间为[kπ+
| π |
| 6 |
| 2π |
| 3 |
（Ⅱ）f（A）=2sin（2A+
| π |
| 6 |
| π |
| 6 |
由于0＜A＜π，则
| π |
| 6 |
| π |
| 6 |
| 13π |
| 6 |
| π |
| 6 |
| π |
| 2 |
则有A=
| π |
| 6 |
由余弦定理得 a2=b2+c2-2bccosA
7=3+c2-3c 即 c2-3c-4=0，即（c-4）（c+1）=0，
解得c=4或c=-1 （不合题意，舍去）
则c=4．
点评：本题考查平面向量的数量积的坐标表示，二倍角公式和两角和的正弦公式，考查正弦函数的单调减区间，考查余弦定理及运用，考查运算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
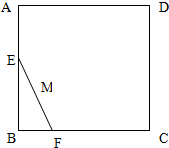如图，线段EF的长度为1，端点E、F在边长不小于1的正方形ABCD的四边上滑动，当E、F沿着正方形的四边滑动一周时，EF的中点M所形成的轨迹为G，若G的周长为L，其围成的面积为S，则L-S的最大值为（ ）| A、4-π | ||
B、2+
| ||
C、
| ||
| D、2π-2 |
下列各式错误的是（ ）
| A、tan138°＜tan143° | ||||
B、sin（-
| ||||
| C、lg1.6＞lg1.4 | ||||
| D、0.75-0.1＜0.750.1 |
已知某几何体的三视图如上图所示（单位：cm），则该几何体的表面积是（ ）
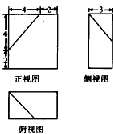
A、（124+2
| ||
| B、92cm2 | ||
| C、124cm2 | ||
| D、84cm2 |