Question

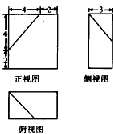
已知某几何体的三视图如上图所示（单位：cm），则该几何体的表面积是（　　）

• A、（124+2

  34

  ）cm²
• B、92cm²
• C、124cm²
• D、84cm²

Answer 1

考点：由三视图求面积、体积

专题：空间位置关系与距离

分析：先由三视图判断出几何体的形状及度量长度，然后求出长方体的表面积，截去棱锥的侧面积，和截面面积，进而求出该几何体的表面积．

解答： 解：由已知中的三视图可得：该几何体是一个长方体，截取一个三棱锥所得的组合体，
由于长方体的长，宽，高，分别为：6，3，6，
故原长方体的表面积为：4×6×3+2×6×6=144cm²，
截去的三棱锥的三个直角三角形侧面面积为：

1

2

×4×4+2×

1

2

×4×3=20cm²，
截面三角形是两腰长为5，底边长为4

2

的等腰三角形，
故底面上的高h=

52-(2 2 )2

=

17

，
即截面面积为：

1

2

×4

2

×

17

=2

34

cm²，
故几何体的表面积S=144-20+2

34

=124+2

34

cm²，
故选：A

点评：解决三视图的题目，关键是由三视图判断出几何体的形状及度量长度，然后利用几何体的面积及体积公式解决．