Question

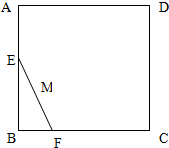如图，线段EF的长度为1，端点E、F在边长不小于1的正方形ABCD的四边上滑动，当E、F沿着正方形的四边滑动一周时，EF的中点M所形成的轨迹为G，若G的周长为L，其围成的面积为S，则L-S的最大值为（　　）

• A、4-π
• B、2+

  2

• C、

  5π

  4

• D、2π-2

Answer 1

考点：函数的最值及其几何意义

专题：计算题,作图题,函数的性质及应用

分析：如图为轨迹G，设正方形ABCD的边长为x，（x≥1），从而得到L=4x-4+2×

1

2

×π=4x-4+π；S=x²-π•

1

22

=x²-

π

4

，从而求最值．

解答： 解：如图为轨迹G，设正方形ABCD的边长为x，（x≥1）；
其中圆弧的半径为

1

2

，
故L=4x-4+2×

1

2

×π
=4x-4+π；
S=x²-π•

1

22

=x²-

π

4

；
故L-S=4x-4+π-（x²-

π

4

）
=-x²+4x+

5π

4

-4；
故当x=2时有最大值，
L-S的最大值为

5π

4

．
故选C．

点评：本题考查了学生的作图能力及函数的最值，属于中档题．