已知△ABC的面积为360.点P是三角形所在平面内一点.且$\overrightarrow{AP}=\frac{1}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$.则△PAB的面积为90．题目和参考答案——青夏教育精英家教网—

题目内容

18．已知△ABC的面积为360，点P是三角形所在平面内一点，且$\overrightarrow{AP}=\frac{1}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$，则△PAB的面积为90．

分析取AB的中点D，AC的中点E，则P为DE的中点，利用相似比，可得结论．

解答解：取AB的中点D，AC的中点E，则P为DE的中点，
∵△ABC的面积为360，
∴△PAB的面积=△ADE的面积=$\frac{1}{4}×360$=90．
故答案为90．

点评本题考查向量知识的运用，考查三角形面积比，考查学生分析解决问题的能力，属于基础题．

练习册系列答案

9．

如图，四棱锥P-ABCD中，AD∥BC，$AB=BC=\frac{1}{2}AD$，E，F，H分别为线段AD，PC，CD的中点，AC与BE交于O点，G是线段OF上一点．
（1）求证：AP∥平面BEF；
（2）求证：GH∥平面PAD．

6．已知正数数列{a_n}的前n项和${S_n}=\frac{1}{4}{（{{a_n}+1}）^2}$，则a_n=2n-1．

13．已知球的半径为R，若球面上两点A，B的球面距离为$\frac{πR}{3}$，则这两点A，B间的距离为R．

3．

已知A是圆锥的顶点，BD是圆锥底面的直径，C是底面圆周上一点，BD=2，BC=1，AC与底面所成角的大小为$\frac{π}{3}$，过点A作截面ABC，ACD，截去部分后的几何体如图所示．
（1）求原来圆锥的侧面积；
（2）求该几何体的体积．

10．

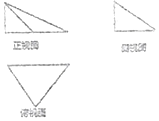一个几何体的三视图如图所示，其中俯视图是一个腰长为2的等腰直角三角形，侧视图是一个直角边长为1的直角三角形，则该几何体外接球的体积是（　　）

7．设直线l过双曲线C的一个焦点，且与C的一条对称轴垂直，l与C交于A，B两点，|AB|为C的实轴长的2倍，则C的离心率为（　　）

8．椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{2}$=1（a＞0）的长轴长为4，则C的离心率为（　　）

试题分类