题目内容
10．
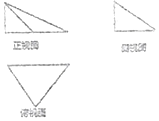一个几何体的三视图如图所示，其中俯视图是一个腰长为2的等腰直角三角形，侧视图是一个直角边长为1的直角三角形，则该几何体外接球的体积是（ ）| A． | 36π | B． | 9π | C． | $\frac{9}{2}π$ | D． | $\frac{27}{5}π$ |
分析 由已知中的三视图可得该几何体是一个三棱锥，求出底面外接圆半径和棱锥的高，进而利用勾股定理，求出其外接球的半径，代入球的体积公式，可得答案．
解答 解：∵俯视图是一个腰长为2的等腰直角三角形，
故底面外接圆半径r=$\sqrt{2}$，
由主视图中棱锥的高h=1，
故棱锥的外接球半径R满足：R=$\sqrt{\frac{1}{4}+2}$=$\frac{3}{2}$，
故该几何体外接球的体积V=$\frac{4}{3}$πR3=$\frac{9}{2}$π，
故选：C．
点评 解决三视图的题目，关键是由三视图判断出几何体的形状及度量长度，进而求出外接球半径，是解答的关键．
练习册系列答案
相关题目
20．抛物线y2=16x的焦点到双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的渐近线的距离是（ ）
| A． | 1 | B． | $\sqrt{3}$ | C． | 2 | D． | 2$\sqrt{3}$ |
1．若集合M={x|（x-1）（x-4）=0}，N={x|（x+1）（x-3）＜0}，则M∩N=（ ）
| A． | ∅ | B． | {1} | C． | {4} | D． | {1，4} |
5．某租车公司给出的财务报表如下：
有投资者在研究上述报表时，发现租车公司有空驶情况，并给出空驶率的计算公式为$T=\frac{t-ak}{ak}•100%$．
（1）分别计算2014，2015年该公司的空驶率的值（精确到0.01%）；
（2）2016年该公司加强了流程管理，利用租车软件，降低了空驶率并提高了平均每单里程，核算截止到11月30日，空驶率在2015年的基础上降低了20个百分点，问2016年前11个月的平均每单油费和平均每单里程分别为多少？（分别精确到0.01元和0.01公里）
 | 1014年（1-12月） | 1015年（1-12月） | 1016年（1-11月） |
| 接单量（单） | 14463272 | 40125125 | 50331996 |
| 油费（元） | 214301962 | 591305364 | 653214963 |
| 平均每单油费t（元） | 14.82 | 14.49 | |
| 平均每单里程k（公里） | 15 | 15 | |
| 每公里油耗a（元） | 0.7 | 0.7 | 0.7 |
（1）分别计算2014，2015年该公司的空驶率的值（精确到0.01%）；
（2）2016年该公司加强了流程管理，利用租车软件，降低了空驶率并提高了平均每单里程，核算截止到11月30日，空驶率在2015年的基础上降低了20个百分点，问2016年前11个月的平均每单油费和平均每单里程分别为多少？（分别精确到0.01元和0.01公里）
19．
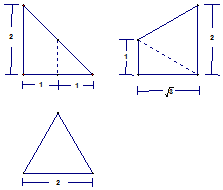如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形，则该几何体的体积（ ）
如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形，则该几何体的体积（ ）| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{2\sqrt{3}}}{3}$ | D． | $\sqrt{3}$ |
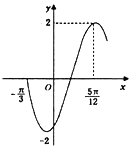函数$f（x）=2sin（{ωx+φ}）（{ω＞0，-\frac{π}{2}＜ω＜\frac{π}{2}}）$的部分图象如图所示，将f（x）的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x．