题目内容
7.设直线l过双曲线C的一个焦点,且与C的一条对称轴垂直,l与C交于A,B两点,|AB|为C的实轴长的2倍,则C的离心率为( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
分析 由于直线l过双曲线的焦点且与对称轴垂直,因此直线l的方程为:x=c或x=-c,代入$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$得y2=b2($\frac{{c}^{2}}{{a}^{2}}$-1)=$\frac{{b}^{4}}{{a}^{2}}$,依题意$\frac{2{b}^{2}}{a}$=4a,即可求出C的离心率.
解答 解:设双曲线的标准方程为$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0),由于直线l过双曲线的焦点且与对称轴垂直,因此直线l的方程为:x=c或x=-c,代入$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$得y2=b2($\frac{{c}^{2}}{{a}^{2}}$-1)=$\frac{{b}^{4}}{{a}^{2}}$,∴y=±$\frac{{b}^{2}}{a}$,
故|AB|=$\frac{2{b}^{2}}{a}$,依题意$\frac{2{b}^{2}}{a}$=4a,∴$\frac{{b}^{2}}{{a}^{2}}$=2,∴e2-1=2,∴e=$\sqrt{3}$.
故选:A.
点评 本题考查双曲线的方程与性质,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
19.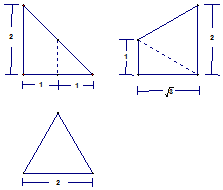 如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积( )
如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积( )
 如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积( )
如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
16.设函数f(x)=-|x|,g(x)=lg(ax2-4x+1),若对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),则实数a的取值范围为( )
| A. | (-2,0] | B. | (0,2] | C. | (-∞,4] | D. | [4,+∞) |