题目内容
8．椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{2}$=1（a＞0）的长轴长为4，则C的离心率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\sqrt{2}$ |
分析 由题意求得a的值，求得椭圆方程，求得a=2，b=$\sqrt{2}$，c=$\sqrt{4-2}$=$\sqrt{2}$，利用椭圆的离心率公式即可求得椭圆的离心率．
解答 解：由椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{2}$=1（a＞0）的长轴长为4，可知焦点在x轴上，
即2a=4，a=2，
∴椭圆的标准方程为：$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$，a=2，b=$\sqrt{2}$，c=$\sqrt{4-2}$=$\sqrt{2}$，
椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$，
故选B．
点评 本题考查椭圆的标准方程及简单几何性质，考查计算能力，属于基础题．
练习册系列答案
备战中考寒假系列答案
相关题目
19．
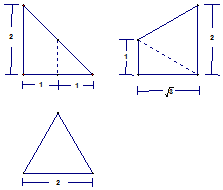如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形，则该几何体的体积（ ）
如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形，则该几何体的体积（ ）| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{2\sqrt{3}}}{3}$ | D． | $\sqrt{3}$ |
16．设函数f（x）=-|x|，g（x）=lg（ax2-4x+1），若对任意x1∈R，都存在x2∈R，使f（x1）=g（x2），则实数a的取值范围为（ ）
| A． | （-2，0] | B． | （0，2] | C． | （-∞，4] | D． | [4，+∞） |
如图，在三棱锥P-ABC中，PA⊥平面ABC，E，F分别为PC，PB中点，∠ACB=90°．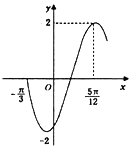
函数$f（x）=2sin（{ωx+φ}）（{ω＞0，-\frac{π}{2}＜ω＜\frac{π}{2}}）$的部分图象如图所示，将f（x）的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x．