题目内容
9. 如图,四棱锥P-ABCD中,AD∥BC,$AB=BC=\frac{1}{2}AD$,E,F,H分别为线段AD,PC,CD的中点,AC与BE交于O点,G是线段OF上一点.
如图,四棱锥P-ABCD中,AD∥BC,$AB=BC=\frac{1}{2}AD$,E,F,H分别为线段AD,PC,CD的中点,AC与BE交于O点,G是线段OF上一点.(1)求证:AP∥平面BEF;
(2)求证:GH∥平面PAD.
分析 (1)连接EC,推导出四边形ABCE是平行四边形,从而FO∥AP,由此能证明AP∥平面BEF.
(2)连接FH,OH,推导出FH∥PD,从而FH∥平面PAD.再求出OH∥AD,从而OH∥平面PAD,进而平面OHF∥平面PAD,由此能证明GH∥平面PAD.
解答 证明:(1)连接EC,∵AD∥BC,$BC=\frac{1}{2}AD$,
∴BC=AE,BC∥AE,∴四边形ABCE是平行四边形,
∴O为AC的中点.
又∵F是PC的中点,∴FO∥AP,
又∵FO?平面BEF,AR?平面BEF,
∴AP∥平面BEF.
(2)连接FH,OH,
∵F,H分别是PC,CD的中点,∴FH∥PD,
又∵PD?平面PAD,FH?平面PAD,
∴FH∥平面PAD.
又∵O是BE的中点,H是CD的中点,
∴OH∥AD,AD?平面PAD,OH?平面PAD,
∴OH∥平面PAD.
又∵FH∩OH=H,∴平面OHF∥平面PAD,
又∵GH?平面OHF,
∴GH∥平面PAD.
点评 本题考查线面平行的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
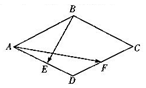
19.菱形ABCD中,E,F分别是AD,CD中点,若∠BAD=60°,AB=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=( )

| A. | $\frac{5}{2}$ | B. | -$\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
20.抛物线y2=16x的焦点到双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的渐近线的距离是( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
14.某程序框图如图所示,执行该程序,若输入4,则输出S=( )


| A. | 10 | B. | 17 | C. | 19 | D. | 36 |
1.若集合M={x|(x-1)(x-4)=0},N={x|(x+1)(x-3)<0},则M∩N=( )
| A. | ∅ | B. | {1} | C. | {4} | D. | {1,4} |
19.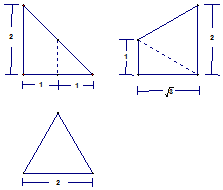 如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积( )
如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积( )
 如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积( )
如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |