题目内容
设函数f(x)=|2x-1|-|x+2|.
(1)求不等式f(x)≥3的解集;
(2)若关于x的不等式f(x)≥t2-3t在[0,1]上无解,求实数t的取值范围.
(1)求不等式f(x)≥3的解集;
(2)若关于x的不等式f(x)≥t2-3t在[0,1]上无解,求实数t的取值范围.
考点:绝对值不等式的解法
专题:计算题,不等式的解法及应用
分析:(1)通过对x范围的分类讨论,去掉绝对值符号,可得f(x)=
,再解不等式f(x)≥3即可求得其解集;
(2)当x∈[0,1]时,易求f(x)max=-1,从而解不等式t2-3t>-1即可求得实数t的取值范围.
|
(2)当x∈[0,1]时,易求f(x)max=-1,从而解不等式t2-3t>-1即可求得实数t的取值范围.
解答:
解:(1)∵f(x)=
,
∴原不等式转化为
或
或
,
解得:x≥6或-2≤x≤-
或x<-2,
∴原不等式的解集为:(-∞,-
]∪[6,+∞);
(2)只要f(x)max<t2-3t,
由(1)知,当x∈[0,1]时,f(x)max=-1,
∴t2-3t>-1,
解得:t>
或t<
.
∴实数t的取值范围为(-∞,
)∪(
,+∞).
|
∴原不等式转化为
|
|
|
解得:x≥6或-2≤x≤-
| 4 |
| 3 |
∴原不等式的解集为:(-∞,-
| 4 |
| 3 |
(2)只要f(x)max<t2-3t,
由(1)知,当x∈[0,1]时,f(x)max=-1,
∴t2-3t>-1,
解得:t>
3+
| ||
| 2 |
3-
| ||
| 2 |
∴实数t的取值范围为(-∞,
3-
| ||
| 2 |
3+
| ||
| 2 |
点评:本题考查绝对值不等式的解法,通过对x范围的分类讨论,去掉绝对值符号是关键,考查转化思想与运算求解能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=
,满足对任意定义域中的x1,x2(x1≠x2),[f(x1)-f(x2)](x1-x2)<0总成立,则实数a的取值范围是( )
|
| A、(-∞,0) |
| B、[-1,0) |
| C、(-1,0) |
| D、(-1,+∞), |
从含有两件正品和一件次品的三件产品中,每次随机取一件,连结取两次,每次取后都放回,则取出的两件产品中恰有一件次的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
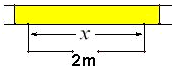 围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:米).
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:米).