Question

已知实数x、y满足（x+2）²+y²=1，求z=

y

x

的最小值及取得最小值时x和y的值．

Answer 1

考点：直线与圆的位置关系

专题：直线与圆

分析：由题意可得z=

y

x

表示圆上的点（x，y）与原点O（0，0）连线的斜率．过原点O作圆C的两条切线，OA、OB，A、B为切点，求得 OA、OB的斜率，可得z=

y

x

的最小值及取得最小值，此时x、y的值即为点A的坐标．

解答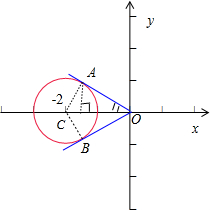： 解：∵实数x、y满足（x+2）²+y²=1，
∴z=

y

x

=

y-0

x-0

 表示圆上的点（x，y）与原点O（0，0）连线的斜率．
如图所示：过原点O作圆的两条切线，OA、OB，A、B为切点，
∵CA=CB=1，OC=2，∴∠AOC=∠BOC=30°，
∴OA的斜率为tan150°=-

3

3

，OB的斜率为tan30°=

3

3

，
故z=

y

x

的最小值及取得最小值为-

3

3

．
此时，x的值即为点A的横坐标：-2+1×cos60°=-

3

2

，
y的值即为点A的纵坐标，为-

3

3

×（-

3

2

）=

3

2

．

点评：本题主要考查直线的斜率公式，直线和圆的位置关系，体现了数形结合的数学思想，属于中档题．