题目内容
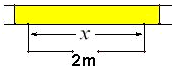围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：米）．（1）将修建围墙的总费用y表示成x的函数；
（2）写出函数f（x）=y的单调区间，并证明．
考点：基本不等式,函数的零点
专题：函数的性质及应用
分析：（1）设矩形的另一边长为am，则根据围建的矩形场地的面积为360m2，易得 a=
，此时再根据旧墙的维修费用为45元/m，新墙的造价为180元/m，我们即可得到修建围墙的总费用y表示成x的函数的解析式；
（2）根据函数的表达式，即可研究函数的单调性．
| 360 |
| x |
（2）根据函数的表达式，即可研究函数的单调性．
解答：
解：（2）设矩形的另一边长为am，
则y=45x+180（x-2）+180•2a=225x+360a-360．
由已知ax=360，得a=
，
∴y=f（x）=225x+
-360，（x＞2）．
（2）∵y=f（x）=225x+
-360，（x＞2）．
∴f'（x）=225-
=
，
则由f’（x）＞0得x＞24，此时函数单调递增，
由f’（x）＜0得2＜x＜24，此时函数单调递减，
故函数的单调递增区间为（24，+∞），
递减区间为（2，24）．
则y=45x+180（x-2）+180•2a=225x+360a-360．
由已知ax=360，得a=
| 360 |
| x |
∴y=f（x）=225x+
| 3602 |
| x |
（2）∵y=f（x）=225x+
| 3602 |
| x |
∴f'（x）=225-
| 3602 |
| x2 |
| 225x2-3602 |
| x2 |
则由f’（x）＞0得x＞24，此时函数单调递增，
由f’（x）＜0得2＜x＜24，此时函数单调递减，
故函数的单调递增区间为（24，+∞），
递减区间为（2，24）．
点评：本题主要考查与函数有关的应用问题，利用条件建立函数关系是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知直线x=a（a＜0）与函数y=（
） x，y=(
)x，y=2x，y=10x的图象依次交与A，B，C，D四点，则这四个点从上到下的排列次序是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| A、A、B、C、D |
| B、B、C、A、D |
| C、B、A、C、D |
| D、C、A、B、D |
随机变量ξ服从二项分布ξ～B（16，P），且Dξ=3，则Eξ等于（ ）
| A、4 | B、12 | C、4或12 | D、3 |
下列函数中，与函数f(x)=
的奇偶性、单调性均相同的是（ ）
| ex-e-x |
| 3 |
A、y=ln(x+
| ||
| B、y=x2 | ||
| C、y=tanx | ||
| D、y=ex |