题目内容
函数f(x)=
,满足对任意定义域中的x1,x2(x1≠x2),[f(x1)-f(x2)](x1-x2)<0总成立,则实数a的取值范围是( )
|
| A、(-∞,0) |
| B、[-1,0) |
| C、(-1,0) |
| D、(-1,+∞), |
考点:函数恒成立问题
专题:计算题,函数的性质及应用
分析:依题意知,f(x)=
为定义域上的减函数,从而得不等式组
,解之即可.
|
|
解答:
解:∵对任意定义域中的x1,x2(x1≠x2),[f(x1)-f(x2)](x1-x2)<0总成立,
∴f(x)=
为定义域上的减函数,
作图如下:

∴
,即
,
∴-1≤a<0,
∴实数a的取值范围是[-1,0),
故选:B.
∴f(x)=
|
作图如下:

∴
|
|
∴-1≤a<0,
∴实数a的取值范围是[-1,0),
故选:B.
点评:本题考查函数恒成立问题,着重考查函数的单调性,考查作图能力与解不等式组的能力,属于中档题.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
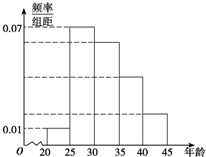 如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图,现已知年龄在[30,35)、[35,40)、[40,45]的上网人数呈现递减的等差数列分布,则年龄在[35,40)的网民出现的频率为( )
如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图,现已知年龄在[30,35)、[35,40)、[40,45]的上网人数呈现递减的等差数列分布,则年龄在[35,40)的网民出现的频率为( )| A、0.04 | B、0.06 |
| C、0.2 | D、0.3 |
若数列{an}的前n项和为Sn,有下列命题:
(1)若数列{an}的极限存在但不为零,则数列{Sn}的极限一定不存在;
(2)无穷数列{S2n}、{S2n-1}的极限均存在,则数列{Sn}的极限一定存在;
(3)若{an}是等差数列(公差d≠0),则S1•S2•…•Sk=O的充要条件是a1•a2•…•ak=O;
(4)若{an}是等比数列,则S1•S2•…•Sk=O(k≥2)的充要条件是an+an+1=0.
其中,错误命题的序号是( )
(1)若数列{an}的极限存在但不为零,则数列{Sn}的极限一定不存在;
(2)无穷数列{S2n}、{S2n-1}的极限均存在,则数列{Sn}的极限一定存在;
(3)若{an}是等差数列(公差d≠0),则S1•S2•…•Sk=O的充要条件是a1•a2•…•ak=O;
(4)若{an}是等比数列,则S1•S2•…•Sk=O(k≥2)的充要条件是an+an+1=0.
其中,错误命题的序号是( )
| A、(1)(2) |
| B、(2)(3) |
| C、(3)(4) |
| D、(1)(4) |
已知直线x=a(a<0)与函数y=(
) x,y=(
)x,y=2x,y=10x的图象依次交与A,B,C,D四点,则这四个点从上到下的排列次序是( )
| 1 |
| 3 |
| 1 |
| 2 |
| A、A、B、C、D |
| B、B、C、A、D |
| C、B、A、C、D |
| D、C、A、B、D |
从某校高三数学学业水平测试卷中随机抽取部分试卷,对其成绩进行分析,因某特殊原因,所得的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,则频率分布直方图中,从左往右第四个矩形的面积为( )
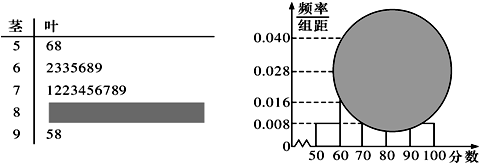

A、
| ||
B、
| ||
C、
| ||
D、
|
等比数列{an}的各项为正数,且3是a5和a6的等比中项,则a1a2…a10=( )
| A、39 |
| B、310 |
| C、311 |
| D、312 |