题目内容
在△ABC中，a、b、c分别为∠A、∠B、∠C的对边，G为△ABC的重心，a•
+b•
+c•
=
．
（1）求
+
+
的值；
（2）判定△ABC的形状．
| GA |
| GB |
| GC |
| 0 |
（1）求
| AG |
| BG |
| CG |
（2）判定△ABC的形状．
考点：向量的加法及其几何意义,正弦定理
专题：平面向量及应用
分析：（1）根据题意，用
、
、
表示出
、
、
，求和即可；
（2）由（1）及a•
+b•
+c•
=
，得出a、b、c的大小关系，从而判定△ABC的形状．
| CB |
| BA |
| CA |
| GA |
| GB |
| GC |
（2）由（1）及a•
| GA |
| GB |
| GC |
| 0 |
解答：
解：（1）如图所示，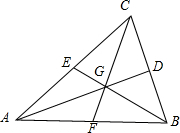
；
在△ABC中，a、b、c分别为∠A、∠B、∠C的对边，G为△ABC的重心，
∴
=
=
（
+
）=
+
，
同理
=
+
，
=
+
，
∴
+
+
=
（
+
+
）+
（
+
+
）
=
（
+
）+
=
+
=
；
（2）∵a•
+b•
+c•
=
，
∴a（
+
）+b（
+
）+c（
+
）=
，
∴（2a-b-c）
+（-a-b+2c）
=
，
所以2a-b-c=0①，-a-b+2c=0②，
由①②得，a=b=c；
∴△ABC为等边三角形．
；在△ABC中，a、b、c分别为∠A、∠B、∠C的对边，G为△ABC的重心，
∴
| GA |
| 2 |
| 3 |
| DA |
| 2 |
| 3 |
| DB |
| BA |
| 1 |
| 3 |
| CB |
| 2 |
| 3 |
| BA |
同理
| GB |
| 1 |
| 3 |
| CA |
| 2 |
| 3 |
| AB |
| GC |
| 1 |
| 3 |
| AB |
| 2 |
| 3 |
| BC |
∴
| GA |
| GB |
| GC |
| 1 |
| 3 |
| CB |
| CA |
| AB |
| 2 |
| 3 |
| BA |
| AB |
| BC |
=
| 1 |
| 3 |
| CB |
| CB |
| 2 |
| 3 |
| BC |
=
| 2 |
| 3 |
| CB |
| 2 |
| 3 |
| BC |
| 0 |
（2）∵a•
| GA |
| GB |
| GC |
| 0 |
∴a（
| 1 |
| 3 |
| CB |
| 2 |
| 3 |
| BA |
| 1 |
| 3 |
| CA |
| 2 |
| 3 |
| AB |
| 1 |
| 3 |
| AB |
| 2 |
| 3 |
| BC |
| 0 |
∴（2a-b-c）
| BA |
| BA |
| 0 |
所以2a-b-c=0①，-a-b+2c=0②，
由①②得，a=b=c；
∴△ABC为等边三角形．
点评：本题考查了平面向量的基本运算问题，解题时应结合图形，是基础题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
从某校高三数学学业水平测试卷中随机抽取部分试卷，对其成绩进行分析，因某特殊原因，所得的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如图，则频率分布直方图中，从左往右第四个矩形的面积为（ ）
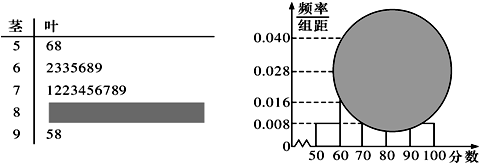
A、
| ||
B、
| ||
C、
| ||
D、
|
在等差数列{an}中，a1=-2012，其前n项和为Sn，若a12-a10=4，则S2012的值等于（ ）
| A、-2010 |
| B、-2011 |
| C、-2012 |
| D、-2013 |