题目内容
从含有两件正品和一件次品的三件产品中,每次随机取一件,连结取两次,每次取后都放回,则取出的两件产品中恰有一件次的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:根据题意用列举法解题,记两件产品中恰有一件是次品为事件A,依次列举所有的基本事件,可得其情况数目,分析可得事件A的情况数目,由等可能事件的概率公式,计算可得答案.
解答:
解:记两件产品中恰有一件是次品为事件A,设依次抽取的两个产品分别记为x,y,则(x,y)表示一次抽取的结果,
基本事件为:(a,a),(b,b),(c,c),(a,b),(b,a),(a,c),(c,a),(b,c),(c,b)共9个;
事件A包含的基本事件(a,c),(c,a),(b,c),(c,b)共4个,
故取出的两件产品中恰有一件次的概率为
,
故选:B.
基本事件为:(a,a),(b,b),(c,c),(a,b),(b,a),(a,c),(c,a),(b,c),(c,b)共9个;
事件A包含的基本事件(a,c),(c,a),(b,c),(c,b)共4个,
故取出的两件产品中恰有一件次的概率为
| 4 |
| 9 |
故选:B.
点评:本题考查等可能事件的概率,涉及列举法的运用;注意本题是有放回抽样,共9种情况.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
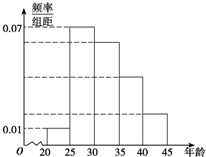 如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图,现已知年龄在[30,35)、[35,40)、[40,45]的上网人数呈现递减的等差数列分布,则年龄在[35,40)的网民出现的频率为( )
如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图,现已知年龄在[30,35)、[35,40)、[40,45]的上网人数呈现递减的等差数列分布,则年龄在[35,40)的网民出现的频率为( )| A、0.04 | B、0.06 |
| C、0.2 | D、0.3 |
等比数列{an}的各项为正数,且3是a5和a6的等比中项,则a1a2…a10=( )
| A、39 |
| B、310 |
| C、311 |
| D、312 |
随机变量ξ服从二项分布ξ~B(16,P),且Dξ=3,则Eξ等于( )
| A、4 | B、12 | C、4或12 | D、3 |
在等差数列{an}中,a1=-2012,其前n项和为Sn,若a12-a10=4,则S2012的值等于( )
| A、-2010 |
| B、-2011 |
| C、-2012 |
| D、-2013 |
下列函数中,与函数f(x)=
的奇偶性、单调性均相同的是( )
| ex-e-x |
| 3 |
A、y=ln(x+
| ||
| B、y=x2 | ||
| C、y=tanx | ||
| D、y=ex |