题目内容
已知函数f(x)=lnx
(1)若方程f(x+a)=x有且只有一个实数解,求a的值;
(2)若函数g(x)=f(x)+
x2-mx(m≥
)的极值点x1,x2(x1<x2)恰好是函数h(x)=f(x)-2x2-bx的零点,记h′(x)为函数h(x)的导函数,求y=(x1-x2)h′(
)的最小值.
(1)若方程f(x+a)=x有且只有一个实数解,求a的值;
(2)若函数g(x)=f(x)+
| 1 |
| 2 |
| 5 |
| 2 |
| x1+x2 |
| 2 |
考点:利用导数研究函数的单调性
专题:函数的性质及应用,导数的综合应用
分析:(1)利用数形结合的思想,根据导数的几何意义,设切点为(x0,x0),继而求出a的值.
(2)先根据函数g(x)=f(x)+
x2-mx(m≥
)的极值点x1,x2求得x1+x2=m,x1•x2=1,再根据极值点x1,x2(x1<x2)恰好是函数h(x)=f(x)-2x2-bx的零点,得到b=-2m+
,再化简y=(x1-x2)h′(
)得到
y=
•(2m+
),判断出在m∈[
,+∞)上为增函数,继而求出y的最小值.
(2)先根据函数g(x)=f(x)+
| 1 |
| 2 |
| 5 |
| 2 |
| 4 |
| m |
| x1+x2 |
| 2 |
y=
| m2-4 |
| 2 |
| m |
| 5 |
| 2 |
解答:
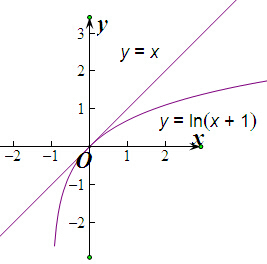 解:(1)∵f(x)=lnx,
解:(1)∵f(x)=lnx,
∴f(x+a)=ln(x+a),x>-a,且x>0,
∴f(x+a)=x有且只有一个实数解,
分别画出函数y=f(x+a)的图象和y=x的图象,如图所示,
当y=f(x+a)的图象和y=x的图象相切时只有一个实数解,
设切点为(x0,x0),
∴k=f′(x0+a)=
=1,①
x0=f(x0+a)=ln(x0+a),②
解得a=1,
(2)∵g(x)=f(x)+
x2-mx=lnx+
x2-mx,
∴g′(x)=
+x-m=
,
令g′(x)=
=0,
得x2-mx+1=0,
∵函数g(x)=f(x)+
x2-mx(m≥
)的极值点x1,x2(x1<x2)
∴x1+x2=m,x1•x2=1,
∴x1-x2=-
∵x1,x2(x1<x2)恰好是函数h(x)=f(x)-2x2-bx的零点,
即h(x)=f(x)-2x2-bx=lnx-2x2-bx=0由两个解分别为x1,x2,
∴h(x1)=lnx1-2x12-bx1=0,③
h(x2)=lnx2-2x22-bx2=0,④
由③+④得lnx1-2x12-bx1+lnx2-2x22-bx2=0,
整理得2m2+bm-4=0,
即b=-2m+
∵h′(x)为函数h(x)的导函数,
∴h′(x)=
-4x-b,
∴h′(
)=
-4(x1+x2)-b,
∴y=(x1-x2)h′(
)=-
•(
-4m-b)=-
•(
-4m+2m-
)=
•(2m+
)
设F(m)=
,G(m)=2m+
,
∴G′(m)=
,
∵m≥
,
∴G′(m)>0,故G(m)=2m+
在m∈[
,+∞)上为增函数,
又F(m)=
在m∈[
,+∞)上为增函数,
∴y=
•(2m+
)在m∈[
,+∞)上为增函数,
∴当m=
时,y有最小值,最小值为ymin=
•(2×
+2×
)=
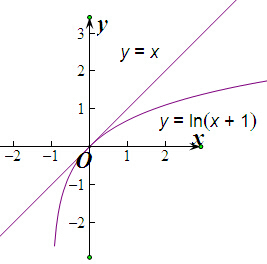 解:(1)∵f(x)=lnx,
解:(1)∵f(x)=lnx,∴f(x+a)=ln(x+a),x>-a,且x>0,
∴f(x+a)=x有且只有一个实数解,
分别画出函数y=f(x+a)的图象和y=x的图象,如图所示,
当y=f(x+a)的图象和y=x的图象相切时只有一个实数解,
设切点为(x0,x0),
∴k=f′(x0+a)=
| 1 |
| x0+a |
x0=f(x0+a)=ln(x0+a),②
解得a=1,
(2)∵g(x)=f(x)+
| 1 |
| 2 |
| 1 |
| 2 |
∴g′(x)=
| 1 |
| x |
| x2-mx+1 |
| x |
令g′(x)=
| x2-mx+1 |
| x |
得x2-mx+1=0,
∵函数g(x)=f(x)+
| 1 |
| 2 |
| 5 |
| 2 |
∴x1+x2=m,x1•x2=1,
∴x1-x2=-
| m2-4 |
∵x1,x2(x1<x2)恰好是函数h(x)=f(x)-2x2-bx的零点,
即h(x)=f(x)-2x2-bx=lnx-2x2-bx=0由两个解分别为x1,x2,
∴h(x1)=lnx1-2x12-bx1=0,③
h(x2)=lnx2-2x22-bx2=0,④
由③+④得lnx1-2x12-bx1+lnx2-2x22-bx2=0,
整理得2m2+bm-4=0,
即b=-2m+
| 4 |
| m |
∵h′(x)为函数h(x)的导函数,
∴h′(x)=
| 1 |
| x |
∴h′(
| x1+x2 |
| 2 |
| 2 |
| x1+x2 |
∴y=(x1-x2)h′(
| x1+x2 |
| 2 |
| m2-4 |
| 2 |
| m |
| m2-4 |
| 2 |
| m |
| 4 |
| m |
| m2-4 |
| 2 |
| m |
设F(m)=
| m2-4 |
| 2 |
| m |
∴G′(m)=
| 2(m2-1) |
| m2 |
∵m≥
| 5 |
| 2 |
∴G′(m)>0,故G(m)=2m+
| 2 |
| m |
| 5 |
| 2 |
又F(m)=
| m2-4 |
| 5 |
| 2 |
∴y=
| m2-4 |
| 2 |
| m |
| 5 |
| 2 |
∴当m=
| 5 |
| 2 |
|
| 5 |
| 2 |
| 2 |
| 5 |
| 87 |
| 10 |
点评:本题主要考查了导数的几何意义,函数的极值点,函数零点的问题,复合函数的单调性,函数最值的问题,关键是求出b与m的关系,培养学生的分析问题,解决问题的能力,本题的计算量较大,属于难题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知全集U={0,2,4,6,8,10},集合A={2,4,6},B={0,2,6,8},则CU(A∩B)为( )
| A、{0,8,10} |
| B、{0,4,8,10} |
| C、{10} |
| D、∅ |
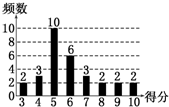 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为me,众数为m0,平均值为
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为me,众数为m0,平均值为. |
| x |
A、me=m0=
| ||
B、me=m0<
| ||
C、me<m0<
| ||
D、m0<me<
|
已知:命题p:“a<b”是“am2<bm2”的充要条件”;命题q:“?x0∈R,x02+x0-2>0”.则下列命题正确的是( )
| A、命题“p∧q”是真命题 |
| B、命题“p∧(¬q)”是真命题 |
| C、命题“(¬p)∧q”是真命题 |
| D、命题“(¬p)∧(¬q)”是真命题 |
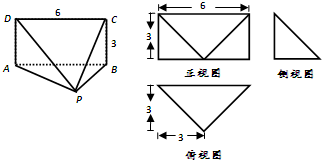
如图是一个几何体的三视图,则该几何体的体积是( )

| A、54 | B、27 | C、18 | D、9 |