题目内容
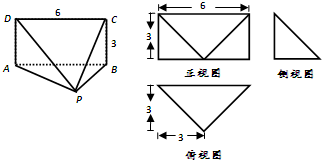
如图是一个几何体的三视图,则该几何体的体积是( )

| A、54 | B、27 | C、18 | D、9 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知的三视图可得:该几何体是一个以正视图为底面的四棱锥,分别求出底面面积和高,代入锥体体积公式,可得答案.
解答:
解:由三视图可知,该几何体是一个以正视图为底面的四棱锥,
∵底面长和宽分别为3和6,
∴其底面面积S=3×6=18,
又∵棱锥的高h=3,
故该几何体的体积V=
Sh=
×3×18=18.
故选:C
∵底面长和宽分别为3和6,
∴其底面面积S=3×6=18,
又∵棱锥的高h=3,
故该几何体的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
故选:C
点评:本题考查的知识点是由三视图求体积和表面积,其中根据三视图分析出几何体的形状是解答的关键.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
下列命题中的假命题是( )
| A、?x∈R,21-x>0 | ||
| B、?x0∈R,当x>x0时,恒有1.1x<x4 | ||
C、?x∈(0,+∞),2x>x
| ||
| D、?α∈R,使函数 y=xα的图象关于y轴对称 |
已知△ABC中,|
|=2,|
|=3,且△ABC的面积为
,则∠BAC=( )
| AB |
| AC |
| 3 |
| 2 |
| A、150° |
| B、120° |
| C、60°或120° |
| D、30°或150° |
已知函数f(x)=x|x-a|+2x,若存在a∈[0,4],使得关于x的方程f(x)=tf(a)有三个不相等的实数根,则实数t的取值范围是( )
A、(1,
| ||||
B、(1,
| ||||
C、(
| ||||
D、(1,
|
若loga
<1,则a的取值范围是( )
| 1 |
| 3 |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(0,
|
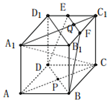 如图正方体ABCD-A1B1C1D1中,E、F分别为D1C1和B1C1的中点,P、Q分别为AC与BD、
如图正方体ABCD-A1B1C1D1中,E、F分别为D1C1和B1C1的中点,P、Q分别为AC与BD、