题目内容
已知在空间四边形ABCD中,E、F分别是AC、BD的中点,且EF=1,AD=BC=2,求异面直线AD与BC所成的角.
考点:异面直线及其所成的角
专题:空间角
分析:如图所示,取AB的中点G,连接EG,FG.又E、F分别是AC、BD的中点,利用三角形的中位线定理可得:∠EGF或其补角即为异面直线AD与BC所成的角.再利用等边三角形的定义即可得出.
解答:
解:如图所示,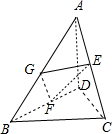
取AB的中点G,连接EG,FG.
又E、F分别是AC、BD的中点,
∴EG
BC,FG
AC,
∴∠EGF或其补角即为异面直线AD与BC所成的角.
又AD=BC=2,EF=1.
∴EG=FG=EF=1,
∴∠EGF=60°.
∴异面直线AD与BC所成的角为60°.

取AB的中点G,连接EG,FG.
又E、F分别是AC、BD的中点,
∴EG
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
∴∠EGF或其补角即为异面直线AD与BC所成的角.
又AD=BC=2,EF=1.
∴EG=FG=EF=1,
∴∠EGF=60°.
∴异面直线AD与BC所成的角为60°.
点评:本题考查了异面直线所成的角、三角形的中位线定理、等边三角形的性质,考查了推理能力,属于基础题.

练习册系列答案
相关题目
集合M={x|2x≤4},N={x|x(1-x)>0},则CMN=( )
| A、(-∞,0)∪[1,+∞] |
| B、(-∞,0)∪[1,2] |
| C、(-∞,0]∪[1,2] |
| D、(-∞,0]∪[1,+∞] |
设双曲线
-
=1(a>0,b>0)的虚轴长为6,焦距为10,则双曲线的实轴长为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、8 | B、6 | C、4 | D、2 |
已知△ABC中,|
|=2,|
|=3,且△ABC的面积为
,则∠BAC=( )
| AB |
| AC |
| 3 |
| 2 |
| A、150° |
| B、120° |
| C、60°或120° |
| D、30°或150° |