题目内容
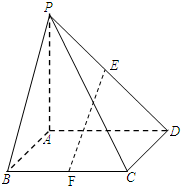 在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点E、F分别是PD、BC的中点.
在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点E、F分别是PD、BC的中点.(1)求证:EF∥平面PAB;
(2)求证:AD⊥PB.
考点:直线与平面垂直的性质,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)做DA的中点M,连接MF,ME,通过中位线的性质证明出EM∥PA,MF∥AB,进而根据线面平行的判定定理、面面平行的判定定理证明出面MEF∥面ABP,继而根据面面平行的性质证明出EF∥平面PAB;
(2)先分别证明出PA⊥AD,PD⊥BC,进而根据线面垂直的判定定理证明出AD⊥平面PAB,即可得出结论.
(2)先分别证明出PA⊥AD,PD⊥BC,进而根据线面垂直的判定定理证明出AD⊥平面PAB,即可得出结论.
解答:
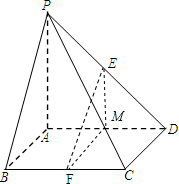 证明:(1)做DA的中点M,连接MF,ME,
证明:(1)做DA的中点M,连接MF,ME,
∵E、F、M均为中点,
∴EM∥PA,MF∥AB,
∵PA?平面PAB,AB?平面PAB,AB∩PA=A,
∴面MEF∥面ABP,
∵EF?面MEF,
∴EF∥平面PAB;
(2)∵PA⊥平面ABCD,AD?平面ABCD,
∴PA⊥AD,
∵底面ABCD为正方形,
∴AD⊥AB.
∵PA∩AB=A,
∴AD⊥平面PAB,
∵PB?平面PAB,
∴AD⊥PB.
 证明:(1)做DA的中点M,连接MF,ME,
证明:(1)做DA的中点M,连接MF,ME,∵E、F、M均为中点,
∴EM∥PA,MF∥AB,
∵PA?平面PAB,AB?平面PAB,AB∩PA=A,
∴面MEF∥面ABP,
∵EF?面MEF,
∴EF∥平面PAB;
(2)∵PA⊥平面ABCD,AD?平面ABCD,
∴PA⊥AD,
∵底面ABCD为正方形,
∴AD⊥AB.
∵PA∩AB=A,
∴AD⊥平面PAB,
∵PB?平面PAB,
∴AD⊥PB.
点评:本题主要考查了线面平行,线面垂直的判定定理的应用.考查了学生对线面平行,线面垂直判定定理的记忆.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
若向量
=(2,3)与
=(m,-6)共线,则实数m=( )
| a |
| b |
| A、-4 | B、4 | C、-9 | D、9 |
已知曲线y=x3+ax+b与斜率为2的直线相切于点A(1,3),则b的值为( )
| A、3 | B、-3 | C、5 | D、-5 |