题目内容
为了庆祝“五一劳动节”,某校教师进行趣味投篮比赛,比赛规则是:每场投5个球,至少投进3个球且最后2个球都投进者获奖;否则不获奖.已知教师甲投进每个球的概率都是
.
(1)记教师甲在每场的5次投球中投进球的个数为X,求X的分布列及数学期望;
(2)求教师甲在一场比赛中获奖的概率.
| 2 |
| 3 |
(1)记教师甲在每场的5次投球中投进球的个数为X,求X的分布列及数学期望;
(2)求教师甲在一场比赛中获奖的概率.
考点:离散型随机变量的期望与方差,互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)X的所有可能值为0,1,2,3,4,5,依条件知X~B(5,
),由此能求出X的分布列及数学期望.(2)设教师甲在一场比赛中获奖的事件为A,利用互斥事件概率加法公式求解.
| 2 |
| 3 |
解答:
解:(1)X的所有可能值为0,1,2,3,4,5,依条件知X~B(5,
),
P(X=k)=
(
)k(
)5-k,k=0,1,2,3,4,5,…(3分)
∴X的分布列为:
EX=5×
=
.…(7分)
(2)设教师甲在一场比赛中获奖的事件为A.
则P(A)=
(
)3(
)2+
(
)4(
)+(
)5=
.…(12分)
| 2 |
| 3 |
P(X=k)=
| C | k 5 |
| 2 |
| 3 |
| 1 |
| 3 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 | 5 | ||||||||||||
| P |
|
|
|
|
|
|
| 2 |
| 3 |
| 10 |
| 3 |
(2)设教师甲在一场比赛中获奖的事件为A.
则P(A)=
| C | 1 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 104 |
| 243 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题.

练习册系列答案
相关题目
在三角形ABC中,A=30°,AB=
,BC=1,则AC=( )
| 3 |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、1或2 |
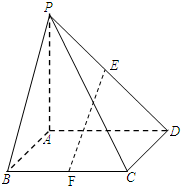 在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点E、F分别是PD、BC的中点.
在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点E、F分别是PD、BC的中点.