题目内容
设F1、F2分别是椭圆
+y2=1的左、右焦点,点P是该椭圆上的一个动点.
(1)求椭圆的离心率
(2)求
•
的最大值与最小值.
| x2 |
| 4 |
(1)求椭圆的离心率
(2)求
| PF1 |
| PF2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由椭圆的方程
+y2=1可得a=2,b=1,再利用c=
可得c,利用椭圆的离心率e=
即可得出;
(2)F1(-
,0),F2(
,0).设P(2cosθ,sinθ)(θ∈∈[0,2π)).利用向量的数量积运算和余弦函数的单调性即可得出.
| x2 |
| 4 |
| a2-b2 |
| c |
| a |
(2)F1(-
| 3 |
| 3 |
解答:
解:(1)由椭圆的方程
+y2=1可得a=2,b=1,∴c=
=
,∴椭圆的离心率e=
=
.
(2)F1(-
,0),F2(
,0).
设P(2cosθ,sinθ)(θ∈∈[0,2π)).
∴
•
═(-
-2cosθ,-sinθ)•(
-2cosθ,-sinθ)=4cos2θ-3+sin2θ=3cos2θ-2,
∵0≤cos2θ≤1,
∴-2≤3cos2θ-2≤1.
即
•
的最大值与最小值分别是1,-2.
| x2 |
| 4 |
| a2-b2 |
| 3 |
| c |
| a |
| ||
| 2 |
(2)F1(-
| 3 |
| 3 |
设P(2cosθ,sinθ)(θ∈∈[0,2π)).
∴
| PF1 |
| PF2 |
| 3 |
| 3 |
∵0≤cos2θ≤1,
∴-2≤3cos2θ-2≤1.
即
| PF1 |
| PF2 |
点评:本题考查了椭圆的标准方程与性质、向量的数量积运算、余弦函数的单调性等基础知识与基本技能方法,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
下列结论正确的是( )
| A、命题“如果p2+q2=2,则p+q≤2”的否命题是“如果p+q>2,则p2+q2≠2” | ||
| B、命题p:?x∈[0,1],ex≥1,命题q:?x∈R,x2+x+1<0,则p∨q为假 | ||
| C、“若am2<bm2,则a<b”的逆命题为真命题 | ||
D、设0<x<
|
为了解甲、乙两批次产品中某微量元素的含量,采用随机抽样的方法从两批次产品中各抽取4件,测得它们所含微量元素(单位:毫克)如表:
根据抽样数据推测( )
| 产品编号 | 1 | 2 | 3 | 4 |
| 甲批产品所含微量元素x | 890 | 890 | 850 | 950 |
| 乙批产品所含微量元素y | 900 | 850 | 910 | 920 |
| A、甲批产品所含微量元素比较稳定 |
| B、乙批产品所含微量元素比较稳定 |
| C、两批产品所含微量元素一样稳定 |
| D、以上判断都不对 |
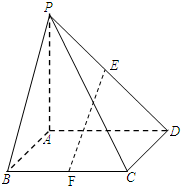 在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点E、F分别是PD、BC的中点.
在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点E、F分别是PD、BC的中点.