题目内容
已知f（x）=
．
（Ⅰ）求f（x）的定义域；
（Ⅱ）设α为第一象限角且tanα=
，求f（α）．
1+
| ||||
| cosx |
（Ⅰ）求f（x）的定义域；
（Ⅱ）设α为第一象限角且tanα=
| 3 |
| 4 |
考点：三角函数中的恒等变换应用
专题：三角函数的求值
分析：（Ⅰ）由余弦函数的性质知，cosx≠0，得x≠kπ+
，k∈Z．从而可得f（x）的定义域；
（Ⅱ）依题意，可求得sinα=
，cosα=
，sin2α=2sinαcosα=
，cos2α=2cos2α-1=
，从而可得f（α）=
的值．
| π |
| 2 |
（Ⅱ）依题意，可求得sinα=
| 3 |
| 5 |
| 4 |
| 5 |
| 24 |
| 25 |
| 7 |
| 25 |
| 1+sin2α+cos2α |
| cosα |
解答：
解：（Ⅰ）由cosx≠0，得x≠kπ+
，k∈Z．
∴f（x）的定义域为{x|x≠kπ+
，k∈Z．}；
（Ⅱ）∵α为第一象限角且tanα=
，不妨设α终边上一点P（4，3），
则|OP|=5，sinα=
，cosα=
，
∴sin2α=2sinαcosα=
，cos2α=2cos2α-1=
，
∴f（α）=
=
=
．
| π |
| 2 |
∴f（x）的定义域为{x|x≠kπ+
| π |
| 2 |
（Ⅱ）∵α为第一象限角且tanα=
| 3 |
| 4 |
则|OP|=5，sinα=
| 3 |
| 5 |
| 4 |
| 5 |
∴sin2α=2sinαcosα=
| 24 |
| 25 |
| 7 |
| 25 |
∴f（α）=
| 1+sin2α+cos2α |
| cosα |
1+
| ||||
|
| 14 |
| 5 |
点评：本题考查三角函数中的恒等变换应用，着重考查同角三角函数间的关系式及二倍角公式的应用，考查三角函数的化简与求值，属于中档题．
练习册系列答案
相关题目
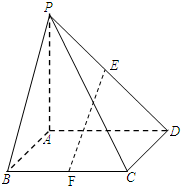在四棱锥P-ABCD中，底面ABCD为正方形，PA⊥平面ABCD，点E、F分别是PD、BC的中点．
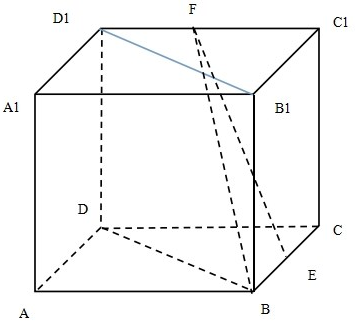如图，在棱长为4的正方体ABCD-A1B1C1D1中，E、F分别是棱BC、C1D1的中点．