题目内容
若向量
=（2，3）与
=（m，-6）共线，则实数m=（ ）
| a |
| b |
| A、-4 | B、4 | C、-9 | D、9 |
考点：平面向量共线（平行）的坐标表示
专题：平面向量及应用
分析：利用向量共线的坐标运算即可得出．
解答：
解：∵
=（2，3）与
=（m，-6）共线，
∴2×（-6）=3m
解得m=-4．
故选：A．
| a |
| b |
∴2×（-6）=3m
解得m=-4．
故选：A．
点评：熟练掌握向量共线的坐标运算是解题的关键．
练习册系列答案
相关题目
已知α∈（
，
），a=log3sinα，b=2sinα，c=2cosα（ ）
| π |
| 4 |
| π |
| 2 |
| A、c＞a＞b |
| B、b＞a＞c |
| C、a＞c＞b |
| D、b＞c＞a |
下列结论正确的是（ ）
| A、命题“如果p2+q2=2，则p+q≤2”的否命题是“如果p+q＞2，则p2+q2≠2” | ||
| B、命题p：?x∈[0，1]，ex≥1，命题q：?x∈R，x2+x+1＜0，则p∨q为假 | ||
| C、“若am2＜bm2，则a＜b”的逆命题为真命题 | ||
D、设0＜x＜
|
设a=
，b=
-
，c=
-
，则a，b，c的大小关系是（ ）
| 2 |
| 7 |
| 3 |
| 6 |
| 2 |
| A、a＞b＞c |
| B、a＞c＞b |
| C、b＞a＞c |
| D、b＞c＞a |
已知（3+
i）•z=4
（i是虚数单位），那么复数z等于（ ）
| 3 |
| 3 |
A、
| ||
B、
| ||
C、3+
| ||
D、3-
|
在三角形ABC中，A=30°，AB=
，BC=1，则AC=（ ）
| 3 |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、1或2 |
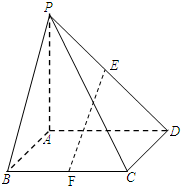在四棱锥P-ABCD中，底面ABCD为正方形，PA⊥平面ABCD，点E、F分别是PD、BC的中点．