题目内容
已知an=2n+1,bn=
,Sn=b12+b22+b32+…+bn2,求证:Sn<
.
| 1 |
| an |
| 1 |
| 4 |
考点:数列的求和
专题:等差数列与等比数列
分析:由
<
(
-
),利用放缩法进行证明.
| 1 |
| (2n+1)2 |
| 1 |
| 2 |
| 1 |
| 2n |
| 1 |
| 2n+2 |
解答:
证明:∵an=2n+1,∴bn=
=
,
∵
<
(
-
),
∴Sn=b12+b22+b32+…+bn2
=
+
+
+…+
<
(
-
+
-
+…+
-
)
=
(
-
)
=
-
<
.
∴Sn<
.
| 1 |
| an |
| 1 |
| 2n+1 |
∵
| 1 |
| (2n+1)2 |
| 1 |
| 2 |
| 1 |
| 2n |
| 1 |
| 2n+2 |
∴Sn=b12+b22+b32+…+bn2
=
| 1 |
| 32 |
| 1 |
| 52 |
| 1 |
| 72 |
| 1 |
| (2n+1)2 |
<
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 2n |
| 1 |
| 2n+2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2n+2 |
=
| 1 |
| 4 |
| 1 |
| 4n+4 |
| 1 |
| 4 |
∴Sn<
| 1 |
| 4 |
点评:本题考查不等式的证明,是中档题,解题时要认真审题,注意放缩法的合理运用.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
已知(3+
i)•z=4
(i是虚数单位),那么复数z等于( )
| 3 |
| 3 |
A、
| ||
B、
| ||
C、3+
| ||
D、3-
|
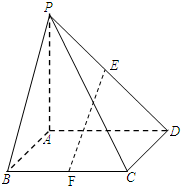 在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点E、F分别是PD、BC的中点.
在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点E、F分别是PD、BC的中点.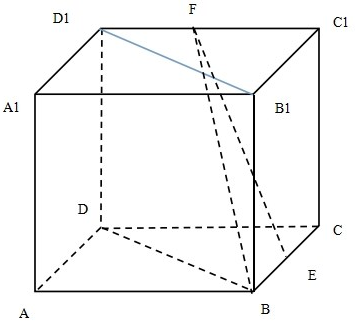 如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是棱BC、C1D1的中点.
如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是棱BC、C1D1的中点.