题目内容
某工厂经过技术改造后,降低了能源消耗,经统计该厂某种产品的产量x(单位:吨)与相应的生产能耗y(单位:吨)有如下几组样本数据:
根据相关性检验,这组样本数据具有线性相关关系,通过线性回归分析,求得回归直线的斜率为0.7.已知该产品的年产量为10吨,则该工厂每年大约消耗的汽油为多少吨?
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
考点:线性回归方程
专题:计算题,概率与统计
分析:求出横标和纵标的平均数,写出样本中心点,把样本中心点代入线性回归方程,得到关于a的方程,解方程,再令x=10即可得出答案.
解答:
解:∵
=
(3+4+5+6)=4.5,
=
(2.5+3+4+4.5)=3.5,
∴这组数据的样本中心点是(4.5,3.5),
把样本中心点代入回归直线方程
=0.7x+a,
∴3.5=4.5×0.7+a,
∴a=0.35,
那么这组数据的回归直线方程是
=0.7x+0.35,
当x=10时,y=0.7×10+0.35=7.35,即该工厂每年大约消耗的汽油为7.35吨.
. |
| x |
| 1 |
| 4 |
. |
| y |
| 1 |
| 4 |
∴这组数据的样本中心点是(4.5,3.5),
把样本中心点代入回归直线方程
| ∧ |
| y |
∴3.5=4.5×0.7+a,
∴a=0.35,
那么这组数据的回归直线方程是
| ∧ |
| y |
当x=10时,y=0.7×10+0.35=7.35,即该工厂每年大约消耗的汽油为7.35吨.
点评:本题考查线性回归方程,解题的关键是线性回归直线一定过样本中心点,这是求解线性回归方程的步骤之一.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
设a=
,b=
-
,c=
-
,则a,b,c的大小关系是( )
| 2 |
| 7 |
| 3 |
| 6 |
| 2 |
| A、a>b>c |
| B、a>c>b |
| C、b>a>c |
| D、b>c>a |





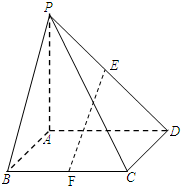 在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点E、F分别是PD、BC的中点.
在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点E、F分别是PD、BC的中点.