题目内容
已知曲线y=x3+ax+b与斜率为2的直线相切于点A（1，3），则b的值为（ ）
| A、3 | B、-3 | C、5 | D、-5 |
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：由曲线y=x3+ax+b与斜率为2的直线相切于点A（1，3），可得：
，解出即可．
|
解答：
解：曲线y=f（x）=x3+ax+b，f′（x）=3x2+a．
∵曲线y=x3+ax+b与斜率为2的直线相切于点A（1，3），
∴
，即
，解得b=-3，a=-1．
故选：B．
∵曲线y=x3+ax+b与斜率为2的直线相切于点A（1，3），
∴
|
|
故选：B．
点评：本题考查了导数的几何意义、切线的斜率，属于基础题．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
已知α∈（
，
），a=log3sinα，b=2sinα，c=2cosα（ ）
| π |
| 4 |
| π |
| 2 |
| A、c＞a＞b |
| B、b＞a＞c |
| C、a＞c＞b |
| D、b＞c＞a |
已知（3+
i）•z=4
（i是虚数单位），那么复数z等于（ ）
| 3 |
| 3 |
A、
| ||
B、
| ||
C、3+
| ||
D、3-
|
在三角形ABC中，A=30°，AB=
，BC=1，则AC=（ ）
| 3 |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、1或2 |
为了解甲、乙两批次产品中某微量元素的含量，采用随机抽样的方法从两批次产品中各抽取4件，测得它们所含微量元素（单位：毫克）如表：
根据抽样数据推测（ ）
| 产品编号 | 1 | 2 | 3 | 4 |
| 甲批产品所含微量元素x | 890 | 890 | 850 | 950 |
| 乙批产品所含微量元素y | 900 | 850 | 910 | 920 |
| A、甲批产品所含微量元素比较稳定 |
| B、乙批产品所含微量元素比较稳定 |
| C、两批产品所含微量元素一样稳定 |
| D、以上判断都不对 |
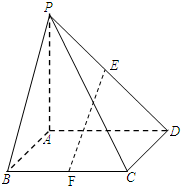在四棱锥P-ABCD中，底面ABCD为正方形，PA⊥平面ABCD，点E、F分别是PD、BC的中点．