题目内容
给出以下五个命题:
①对于任意的a>0,b>0,都有algb=blga成立;
②直线y=x•tanα+b的倾斜角等于α;
③与两条异面直线都平行且距离相等的平面有且只有一个;
④在平面内,如果将单位向量的起点移到同一个点,那么终点的轨迹是一个半径为1的圆;
⑤已知函数y=f(x),若存在常数M>0,使|f(x)|<M•|x|对定义域内的任意x均成立,则称f(x)为“倍约束函数”.对于二次函数f(x)=x2+1,该函数是倍约束函数.
其中真命题的序号是 .
①对于任意的a>0,b>0,都有algb=blga成立;
②直线y=x•tanα+b的倾斜角等于α;
③与两条异面直线都平行且距离相等的平面有且只有一个;
④在平面内,如果将单位向量的起点移到同一个点,那么终点的轨迹是一个半径为1的圆;
⑤已知函数y=f(x),若存在常数M>0,使|f(x)|<M•|x|对定义域内的任意x均成立,则称f(x)为“倍约束函数”.对于二次函数f(x)=x2+1,该函数是倍约束函数.
其中真命题的序号是
考点:命题的真假判断与应用
专题:综合题
分析:①中,由a>0,b>0得出lgalgb=lgblga=lga•lgb,判定①正确;
②中,由当且仅当α∈[0,
)∪(
,π)时,直线y=x•tanα+b的倾斜角等于α,判定②错误;
③中,由分别过两异面直线a,b作平面α,β,能使α∥β的平面有且仅有一对,得出③正确;
④中,由平面内单位向量的起点在同一点时,它终点的轨迹是一个半径为1的圆,判定④正确;
⑤中,举例说明二次函数f(x)=x2+1不是倍约束函数,从而判定⑤错误.
②中,由当且仅当α∈[0,
| π |
| 2 |
| π |
| 2 |
③中,由分别过两异面直线a,b作平面α,β,能使α∥β的平面有且仅有一对,得出③正确;
④中,由平面内单位向量的起点在同一点时,它终点的轨迹是一个半径为1的圆,判定④正确;
⑤中,举例说明二次函数f(x)=x2+1不是倍约束函数,从而判定⑤错误.
解答:
解:对于①,当a>0,b>0时,∵blga>0,algb>0,∴lgalgb=lgb•lga,lgblga=lga•lgb,∴algb=blga;∴①正确;
对于②,当α∈[0,
)∪(
,π)时,直线y=x•tanα+b的倾斜角等于α,否则不等于;∴②错误;
对于③,分别过两条异面直线a,b作平面α,β,其中能使α∥β的平面有且仅有一对;
若要作一平面与两异面直线同时平行且距离相等,则所作平面必须与α,β同时平行且距离相等,这样的平面有且只有一个;∴③正确;
对于④,在平面内,将单位向量的起点移到同一个点,它终点的轨迹是一个半径为1的圆;∴④正确;
对于⑤,∵f(0)=1,|f(0)|=M•0=0,不满足|f(x)|≤M•|x|,∴二次函数f(x)=x2+1不是倍约束函数,⑤错误.
综上,正确的命题有①③④.
故答案为:①③④.
对于②,当α∈[0,
| π |
| 2 |
| π |
| 2 |
对于③,分别过两条异面直线a,b作平面α,β,其中能使α∥β的平面有且仅有一对;
若要作一平面与两异面直线同时平行且距离相等,则所作平面必须与α,β同时平行且距离相等,这样的平面有且只有一个;∴③正确;
对于④,在平面内,将单位向量的起点移到同一个点,它终点的轨迹是一个半径为1的圆;∴④正确;
对于⑤,∵f(0)=1,|f(0)|=M•0=0,不满足|f(x)|≤M•|x|,∴二次函数f(x)=x2+1不是倍约束函数,⑤错误.
综上,正确的命题有①③④.
故答案为:①③④.
点评:本题通过命题真假的判定,考查了对数的运算性质,直线的斜率与倾斜角的关系,空间中的两条异面直线的概念以及应用,平面向量的知识和新定义的问题应用等知识,是综合题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在函数①y=cos丨2x丨,②y=丨cosx丨,③y=cos(2x+
)④y=tan(2x-
)中,最小正周期为π的所有函数为( )
| π |
| 6 |
| π |
| 4 |
| A、①②③ | B、①③④ |
| C、②④ | D、①③ |
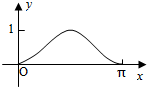
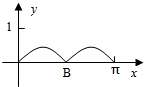
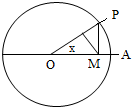 如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P做直线OA的垂线,垂足为M,将点M到直线OP的距离表示为x的函数f(x),则y=f(x)在[0,π]的图象大致为( )
如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P做直线OA的垂线,垂足为M,将点M到直线OP的距离表示为x的函数f(x),则y=f(x)在[0,π]的图象大致为( )