题目内容
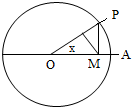 如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P做直线OA的垂线,垂足为M,将点M到直线OP的距离表示为x的函数f(x),则y=f(x)在[0,π]的图象大致为( )
如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P做直线OA的垂线,垂足为M,将点M到直线OP的距离表示为x的函数f(x),则y=f(x)在[0,π]的图象大致为( )A、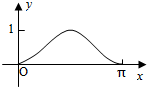 |
B、 |
C、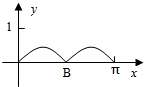 |
D、 |
考点:抽象函数及其应用
专题:三角函数的图像与性质
分析:在直角三角形OMP中,求出OM,注意长度、距离为正,再根据直角三角形的锐角三角函数的定义即可得到f(x)的表达式,然后化简,分析周期和最值,结合图象正确选择.
解答:
解:在直角三角形OMP中,OP=1,∠POM=x,则OM=|cosx|,
∴点M到直线OP的距离表示为x的函数f(x)=OM|sinx|
=|cosx|•|sinx|=
|sin2x|,
其周期为T=
,最大值为
,最小值为0,
故选C.
∴点M到直线OP的距离表示为x的函数f(x)=OM|sinx|
=|cosx|•|sinx|=
| 1 |
| 2 |
其周期为T=
| π |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题主要考查三角函数的图象与性质,正确表示函数的表达式是解题的关键,同时考查二倍角公式的运用.

练习册系列答案
相关题目
下列函数中,定义域是R且为增函数的是( )
| A、y=e-x |
| B、y=x |
| C、y=lnx |
| D、y=|x| |
阅读如图所示的程序框图,运行相应的程序,输出的n的值为( )
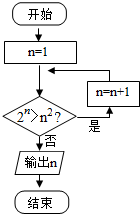

| A、1 | B、2 | C、3 | D、4 |
设x,y满足约束条件
,则z=x+2y的最大值为( )
|
| A、8 | B、7 | C、2 | D、1 |
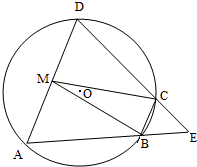 如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.