题目内容
已知集合A={3，4，5，12，13}，B={2，3，5，8，13}，则A∩B= ．
考点：交集及其运算
专题：计算题
分析：根据题意，分析集合A、B的公共元素，由交集的意义即可得答案．
解答：
解：根据题意，集合A={3，4，5，12，13}，B={2，3，5，8，13}，
A、B公共元素为3、5、11，
则A∩B={3，5，13}，
故答案为：{3，5，13}．
A、B公共元素为3、5、11，
则A∩B={3，5，13}，
故答案为：{3，5，13}．
点评：本题考查集合交集的运算，注意写出集合的形式．
练习册系列答案
阅读快车系列答案
相关题目
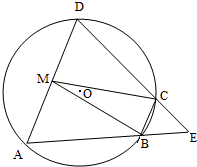如图，四边形ABCD是⊙O的内接四边形，AB的延长线与DC的延长线交于点E，且CB=CE．（Ⅰ）证明：∠D=∠E；
（Ⅱ）设AD不是⊙O的直径，AD的中点为M，且MB=MC，证明：△ADE为等边三角形．
如图，某公司要在A、B两地连线上的定点C处建造广告牌CD，其中D为顶端，AC长35米，CB长80米，设点A、B在同一水平面上，从A和B看D的仰角分别为α和β．
在（1+x）6（1+y）4的展开式中，记xmyn项的系数为f（m，n），则f（3，0）+f（2，1）+f（1，2）+f（0，3）=（ ）
| A、45 | B、60 |
| C、120 | D、210 |