题目内容
在△ABC中,内角A,B,C所对的边分别为a,b,c,已知4sin2
+4sinAsinB=2+
.
(Ⅰ)求角C的大小;
(Ⅱ)已知b=4,△ABC的面积为6,求边长c的值.
| A-B |
| 2 |
| 2 |
(Ⅰ)求角C的大小;
(Ⅱ)已知b=4,△ABC的面积为6,求边长c的值.
考点:二倍角的余弦,两角和与差的正弦函数,余弦定理
专题:解三角形
分析:(Ⅰ)△ABC中由条件利用二倍角的余弦公式、两角和的余弦公式求得cos(A+B)=-
,从而得到cosC=
,由此可得C的值.
(Ⅱ)根据△ABC的面积为6=
ab•sinC求得a的值,再利用余弦定理求得c=
的值.
| ||
| 2 |
| ||
| 2 |
(Ⅱ)根据△ABC的面积为6=
| 1 |
| 2 |
| a2+b2-2ab•cosC |
解答:
解:(Ⅰ)△ABC中,∵4sin2
+4sinAsinB=2+
,∴4×
+4sinAsinB=2+
,
∴-2cosAcosB+2sinAsinB=
,即 cos(A+B)=-
,
∴cosC=
,∴C=
.
(Ⅱ)已知b=4,△ABC的面积为6=
ab•sinC=
a×4×
,∴a=3
,
∴c=
=
=
.
| A-B |
| 2 |
| 2 |
| 1-cos(A-B) |
| 2 |
| 2 |
∴-2cosAcosB+2sinAsinB=
| 2 |
| ||
| 2 |
∴cosC=
| ||
| 2 |
| π |
| 4 |
(Ⅱ)已知b=4,△ABC的面积为6=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
∴c=
| a2+b2-2ab•cosC |
18+16-2×3
|
| 10 |
点评:本题主要考查二倍角的余弦公式、两角和差的三角公式、余弦定理的应用,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
下列函数中,定义域是R且为增函数的是( )
| A、y=e-x |
| B、y=x |
| C、y=lnx |
| D、y=|x| |
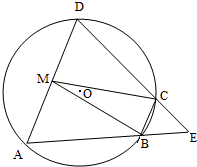 如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE. 如图,某公司要在A、B两地连线上的定点C处建造广告牌CD,其中D为顶端,AC长35米,CB长80米,设点A、B在同一水平面上,从A和B看D的仰角分别为α和β.
如图,某公司要在A、B两地连线上的定点C处建造广告牌CD,其中D为顶端,AC长35米,CB长80米,设点A、B在同一水平面上,从A和B看D的仰角分别为α和β.