题目内容

从编号1，2，3，4的四个球中任取（无放回，且每球取到的机会均等）两个球，则1号球被取到的概率为
 
．
考点：等可能事件的概率
专题：计算题,概率与统计
分析：求得从编号1，2，3，4的四个球中任取（无放回，且每球取到的机会均等）两个球、1号球被取到的情况，利用古典概型概率公式求解即可．
解答： 解：从编号1，2，3，4的四个球中任取（无放回，且每球取到的机会均等）两个球，共有
C
2
4
=6种情况，1号球被取到有3种情况，
∴1号球被取到的概率为
3
6
=0.5．
故答案为：0.5．
点评：本题考查古典概型，是一个古典概型与排列组合结合的问题，解题时先要判断该概率模型是不是古典概型，再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数．
练习册系列答案
相关题目
已知直线l的参数方程为
x=a-2t
y=-4t
（t为参数），圆C的参数方程为
x=4cosθ
y=4sinθ
（θ为常数）．
（1）求直线l和圆C的普通方程；
（2）若直线l与圆C有公共点，求实数a的取值范围．
设数列{an}的前n项和为Sn，若对任意的正整数n，总存在正整数m，使得Sn=am，则称{an}是“H数列”．
（1）若数列{an}的前n项和为Sn=2n（n∈N*），证明：{an}是“H数列”；
（2）设{an}是等差数列，其首项a1=1，公差d＜0，若{an}是“H数列”，求d的值；
（3）证明：对任意的等差数列{an}，总存在两个“H数列”{bn}和{cn}，使得an=bn+cn（n∈N*）成立．
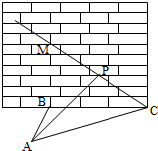如图，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练．已知点A到墙面的距离为AB，某目标点P沿墙面上的射线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小．若AB=15m，AC=25m，∠BCM=30°，则tanθ的最大值是
 
．（仰角θ为直线AP与平面ABC所成角）
给出以下五个命题：
①对于任意的a＞0，b＞0，都有algb=blga成立；
②直线y=x•tanα+b的倾斜角等于α；
③与两条异面直线都平行且距离相等的平面有且只有一个；
④在平面内，如果将单位向量的起点移到同一个点，那么终点的轨迹是一个半径为1的圆；
⑤已知函数y=f（x），若存在常数M＞0，使|f（x）|＜M•|x|对定义域内的任意x均成立，则称f（x）为“倍约束函数”．对于二次函数f（x）=x2+1，该函数是倍约束函数．
其中真命题的序号是
 
．
分别在区间[1，6]和[1，4]内任取一个实数，依次记为m和n，则m＞n的概率为
 
．
在某程序框图如图所示，当输入50时，则该程序运算后输出的结果是
 
．
若变量 x，y满足约束条件
x-y+1≤0
x+2y-8≤0
x≥0
，则z=3x+y的最小值为
 
．
.
z
是z的共轭复数，若z+
.
z
=2，（z-
.
z
）i=2（i为虚数单位），则z=（　　）
A、1+iB、-1-i
C、-1+iD、1-i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网