题目内容
设函数f(x)=kax-a-x(a>0且a≠1)是定义域为R的奇函数;
(1)若f(1)>0,判断f(x)的单调性并求不等式f(x+2)+f(x-4)>0的解集;
(2)若f(1)=
,且g(x)=a2x+a-2x-4f(x),求g(x)在[1,+∞)上的最小值.
(1)若f(1)>0,判断f(x)的单调性并求不等式f(x+2)+f(x-4)>0的解集;
(2)若f(1)=
| 3 |
| 2 |
考点:指数函数综合题,函数单调性的性质,函数奇偶性的性质
专题:综合题,函数的性质及应用
分析:由题意,先由奇函数的性质得出k的值,
(1)由f(1)>0求出a的范围,得出函数的单调性,利用单调性解不等式;
(2)f(1)=
得出a的值,将函数变为g(x)=22x+2-2x-4 (2x-2-x)=(2x-2-x)2-4(2x-2-x)+2,再利用换元法求出函数的最小值.
(1)由f(1)>0求出a的范围,得出函数的单调性,利用单调性解不等式;
(2)f(1)=
| 3 |
| 2 |
解答:
解:函数f(x)=kax-a-x(a>0且a≠1)是定义域为R的奇函数,可得f(0)=0,从而得k-1=0,即k=1.
(1)由f(1)>0可得a-
>0,解得a>1,所以f(x)=ax-a-x是增函数,
由f(x+2)+f(x-4)>0可得f(x+2)>-f(x-4)=f(4-x),
所以x+2>4-x,解得x>3,
即不等式的解集是(3,+∞).
(2)f(1)=
得a-
=
,解得a=2,故g(x)=22x+2-2x-4 (2x-2-x)=(2x-2-x)2-4(2x-2-x)+2,
令t=2x-2-x,它在[1,+∞)上是增函数,故t≥
,即g(x)=t2-4t+2,t≥
.
此函数的对称轴是t=2≥
,故最小值为22-4×2+2=-2.
(1)由f(1)>0可得a-
| 1 |
| a |
由f(x+2)+f(x-4)>0可得f(x+2)>-f(x-4)=f(4-x),
所以x+2>4-x,解得x>3,
即不等式的解集是(3,+∞).
(2)f(1)=
| 3 |
| 2 |
| 1 |
| a |
| 3 |
| 2 |
令t=2x-2-x,它在[1,+∞)上是增函数,故t≥
| 3 |
| 2 |
| 3 |
| 2 |
此函数的对称轴是t=2≥
| 3 |
| 2 |
点评:本题考查指数函数与奇偶性单调性结合的题,综合性强,本题第二小题考查复函数最值的求法,换元法解此类题可大大降低难度.

练习册系列答案
相关题目
二次不等式ax2+bx+c<0的解集为{x|x≠-
}的条件为( )
| b |
| 2a |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
若角A是三角形的一个内角,且sinAcosA<0,则这个三角形的形状是( )
| A、锐角三角形 |
| B、钝角三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
等比数列{an}中,a1•a5=16,则a3=( )
| A、8 | B、4 | C、-4 | D、±4 |
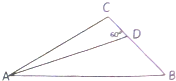 爸爸去哪儿节目组安排星娃们露营,村长要求,Feyman、杨阳洋、贝儿依次在A、B、C三处扎帐篷,AB=8米,BC=4米,AC=6米.现村长给多多一个难题,要求她安扎在B、C两点连线段上的D点位置,∠ADC=60°,如图所示,问多多与Feyman相距多少米?
爸爸去哪儿节目组安排星娃们露营,村长要求,Feyman、杨阳洋、贝儿依次在A、B、C三处扎帐篷,AB=8米,BC=4米,AC=6米.现村长给多多一个难题,要求她安扎在B、C两点连线段上的D点位置,∠ADC=60°,如图所示,问多多与Feyman相距多少米?