题目内容
已知定义在R上的函数f(x)对任意x,y∈R均有:f(x+y)+f(x-y)=2f(x)f(y)且f(x)不恒为零.则下列结论正确的是
①f(0)=0
②f(0)=1
③f(0)=0或f(0)=1
④函数f(x)为偶函数
⑤若存在实数a≠0使f(a)=0,则f(x)为周期函数且2a为其一个周期.
①f(0)=0
②f(0)=1
③f(0)=0或f(0)=1
④函数f(x)为偶函数
⑤若存在实数a≠0使f(a)=0,则f(x)为周期函数且2a为其一个周期.
考点:函数的周期性,抽象函数及其应用
专题:计算题,函数的性质及应用
分析:由f(x+y)+f(x-y)=2f(x)f(y)且f(x)不恒为零,可解出f(0)=1,故可判断①②③④;代入f(a)=0求函数的周期即可.
解答:
解:由f(x)不恒为零,若f(0)=0,则f(x)+f(x)=0,故①错误;
令x=y=0,则f(0)+f(0)=2f(0)•f(0),
解得,f(0)=1,②正确;
由以上知,③错误;
令x=0,则f(y)+f(-y)=2f(y),
即f(-y)=f(y),又∵定义域为R;
故④正确;
由题意,f(x+a)+f(x-a)=0,
则f(x+a)=-f(x-a)=f(x-3a),
故4a是其一个周期;
故⑤不正确;
故答案为:②④.
令x=y=0,则f(0)+f(0)=2f(0)•f(0),
解得,f(0)=1,②正确;
由以上知,③错误;
令x=0,则f(y)+f(-y)=2f(y),
即f(-y)=f(y),又∵定义域为R;
故④正确;
由题意,f(x+a)+f(x-a)=0,
则f(x+a)=-f(x-a)=f(x-3a),
故4a是其一个周期;
故⑤不正确;
故答案为:②④.
点评:本题考查了抽象函数的函数值及周期性判断,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
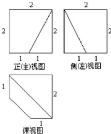
已知一个棱长为2的正 方体,被一个平面截后所得几何体的三视图如图所示,则该截面的面积为( )

A、
| ||||
| B、4 | ||||
C、
| ||||
| D、5 |
对于函数f(x)=
,下列命题正确的是( )
|
| A、值域[-1,1] | ||
B、当且仅当x=2kπ+
| ||
| C、最小正周期为π | ||
D、当且仅当2kπ+π<x<2kπ+
|
曲线y=x2-x+1在点(1,0)处的切线方程为( )
| A、y=x-1 |
| B、y=-x+1 |
| C、y=2x-2 |
| D、y=-2x+2 |
求解不等式组
( )
|
| A、{x|-3<x≤5} |
| B、{x|-3≤x<5} |
| C、{x|-3≤x≤5} |
| D、∅ |
