题目内容
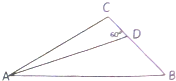 爸爸去哪儿节目组安排星娃们露营,村长要求,Feyman、杨阳洋、贝儿依次在A、B、C三处扎帐篷,AB=8米,BC=4米,AC=6米.现村长给多多一个难题,要求她安扎在B、C两点连线段上的D点位置,∠ADC=60°,如图所示,问多多与Feyman相距多少米?
爸爸去哪儿节目组安排星娃们露营,村长要求,Feyman、杨阳洋、贝儿依次在A、B、C三处扎帐篷,AB=8米,BC=4米,AC=6米.现村长给多多一个难题,要求她安扎在B、C两点连线段上的D点位置,∠ADC=60°,如图所示,问多多与Feyman相距多少米?考点:解三角形的实际应用
专题:应用题,解三角形
分析:利用余弦定理求出cosC,可得sinC,再利用正弦定理,即可得出结论.
解答:
解:由余弦定理可得cosC=
=
,
∴sinC=
,
由正弦定理可得
=
,
∴|AD|=3
米,
故多多与Feyman相距3
米.
| 16+36-64 |
| 2×4×6 |
| 1 |
| 4 |
∴sinC=
| ||
| 4 |
由正弦定理可得
| |AD| | ||||
|
| 6 | ||||
|
∴|AD|=3
| 5 |
故多多与Feyman相距3
| 5 |
点评:本题考查解三角形的实际应用,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
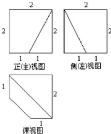
已知一个棱长为2的正 方体,被一个平面截后所得几何体的三视图如图所示,则该截面的面积为( )

A、
| ||||
| B、4 | ||||
C、
| ||||
| D、5 |
函数f(x)=lnx-
的零点所在的区间是( )
| 3 |
| x |
| A、(1,2) |
| B、(1,e) |
| C、(e,3) |
| D、(e,+∞) |
若直线2x-y+a=0过圆x2+y2-2x+6y=0的圆心,则a的值为( )
| A、4 | B、-4 | C、-5 | D、-6 |
对于函数f(x)=
,下列命题正确的是( )
|
| A、值域[-1,1] | ||
B、当且仅当x=2kπ+
| ||
| C、最小正周期为π | ||
D、当且仅当2kπ+π<x<2kπ+
|
曲线y=x2-x+1在点(1,0)处的切线方程为( )
| A、y=x-1 |
| B、y=-x+1 |
| C、y=2x-2 |
| D、y=-2x+2 |
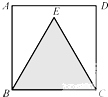 如图,正方形ABCD的边长为2,△EBC为正三角形.若向正方形ABCD内随机投掷一个质点,则它落在△EBC内的概率为
如图,正方形ABCD的边长为2,△EBC为正三角形.若向正方形ABCD内随机投掷一个质点,则它落在△EBC内的概率为