题目内容
6.设f(x)=asin(πx+α)+bcos(πx+β),其中a,b,α,β∈R,且ab≠0,α≠kπ(k∈Z),若f(2015)=5,则f(2016)=-5.分析 利用诱导公式化简已知条件,转化求解即可.
解答 解:f(x)=asin(πx+α)+bcos(πx+β),其中a,b,α,β∈R,且ab≠0,α≠kπ(k∈Z),
f(2015)=5,
可得:f(2015)=asin(2015π+α)+bcos(2015π+β)=-asinα-bcosβ=5,
f(2016)=asin(2016π+α)+bcos(2016π+β)=asinα+bcosβ=-5,
故答案为:-5.
点评 本题考查诱导公式的应用,三角函数的恒等变形化简求值,考查计算能力.

练习册系列答案
相关题目
18.下列函数中,图象与函数y=4x的图象关于y轴对称的是( )
| A. | y=-4x | B. | y=4-x | C. | y=-4-x | D. | y=4x+4-x |
16.已知角θ的终边经过点$P(-\frac{1}{2},\frac{{\sqrt{3}}}{2})$,则tanθ的值为( )
| A. | $-\sqrt{3}$ | B. | -$\frac{{\sqrt{3}}}{3}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
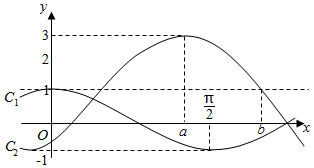 函数f(x)=Asin($ωx-\frac{π}{3}$)+1(A>0,ω>0)与g(x)=cosωx的部分图象如图所示.
函数f(x)=Asin($ωx-\frac{π}{3}$)+1(A>0,ω>0)与g(x)=cosωx的部分图象如图所示. 已知函数f(x)=2|x+1|-|x-2|,x∈[-3,3].
已知函数f(x)=2|x+1|-|x-2|,x∈[-3,3].