题目内容
15．已知m，n∈N+，在（1+x）m（1+y+2z）n的展开式中，若x3y3的系数不小90，则m+n的最小值为13．分析 由题意可得 ${C}_{m}^{3}$•${C}_{n}^{3}$≥90，可得m≥3，n≥3，由此可得m+n的最小值．
解答 解：在（1+x）m（1+y+2z）n的展开式中，若x3y3的系数不小90，即 ${C}_{m}^{3}$•${C}_{n}^{3}$≥90，
∴m≥3，n≥3，∴m+n≥6，当m=3，n=9，${C}_{m}^{3}$•${C}_{n}^{3}$=84＜90；m=3，n=10时，${C}_{m}^{3}$•${C}_{n}^{3}$=120＞90；故m+n的最小值为13，
故答案为：13．
点评 本题主要考查二项式定理的应用，组合数的性质．
练习册系列答案
金钥匙试卷系列答案
相关题目
15．若实数x，y∈R，则“x＞0，y＞0”是“x+y＞0”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
3．《九章算术》中有如下问题：“今有勾八步，股一十五步，问勾中容圆，径几何？”其大意：“已知直角三角形两直角边长分别为8步和15步，问其内切圆的直径为多少步？”现若向此三角形内随机投一粒豆子，则豆子落在其内切圆外的概率是（ ）
| A． | $\frac{3π}{10}$ | B． | $\frac{3π}{20}$ | C． | $1-\frac{3π}{10}$ | D． | $1-\frac{3π}{20}$ |
10．若由一个2×2列联表中的数据计算得K2的观测值k≈6.630，则判断“这两个分类变量有关系”时，犯错误的最大概率是0.025．
参考数据：
参考数据：
| P（K2≥k0） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
20．若数列{an}满足a1=1，log2an+1=log2an+1（n∈N*），它的前n项和为Sn，则Sn=（ ）
| A． | 2-21-n | B． | 2n-1-1 | C． | 2n-1 | D． | 2-2n-1 |
7．在下列条件中，可以判断三角形有两解的是（ ）
| A． | A=30°．B=45°．c=10 | B． | a=$\sqrt{3}$．c=$\sqrt{2}$．B=45° | ||
| C． | a=14．c=16．A=45° | D． | c=7．b=5．C=80° |
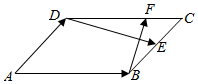如图，在平行四边形ABCD中，E，F分别是BC，DC上的点，且满足$\overrightarrow{BE}$=$\overrightarrow{EC}$，$\overrightarrow{DF}$=2$\overrightarrow{FC}$，记$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AD}=\overrightarrow b$，试以$\overrightarrow a，\overrightarrow b$为平面向量的一组基底．利用向量的有关知识解决下列问题；