题目内容
6.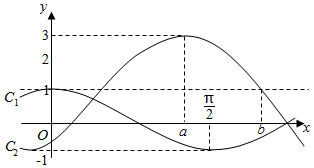 函数f(x)=Asin($ωx-\frac{π}{3}$)+1(A>0,ω>0)与g(x)=cosωx的部分图象如图所示.
函数f(x)=Asin($ωx-\frac{π}{3}$)+1(A>0,ω>0)与g(x)=cosωx的部分图象如图所示.(1)求A,a,b的值及函数f(x)的递增区间;
2)若函数y=g(x-m)(m>π)与y=f(x)+f(x-$\frac{π}{4}$)的图象的对称轴完全相同,求m的最小值.
分析 (1)根据g(x)=cosωx的部分图象的周期性求得ω,由函数f(x)的图象的顶点坐标求出A,由周期求出a、b的值,由正弦函数的单调性求得函数f(x)的递增区间.
(2)先化简g(x-m)、y=f(x)+f(x-$\frac{π}{4}$)的解析式,再结合正弦函数、余弦函数的图象特征,求得m的最小值.
解答 解:(1)根据g(x)=cosωx的部分图象可得ω•$\frac{π}{2}$=π,∴ω=2.
再根据函数f(x)=Asin($ωx-\frac{π}{3}$)+1(A>0,ω>0)的部分图象,可得A=$\frac{3-(-1)}{2}$=2,
$\frac{1}{4}$•$\frac{2π}{ω}$=$\frac{π}{4}$=b-a,ωa-$\frac{π}{3}$=2a-$\frac{π}{3}$=$\frac{π}{2}$,ωb-$\frac{π}{3}$=2b-$\frac{π}{3}$=π.∴a=$\frac{5π}{12}$,b=$\frac{2π}{3}$,
∴f(x)=Asin($ωx-\frac{π}{3}$)+1=2sin(2x-$\frac{π}{3}$)+1.
令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5π}{12}$,
可得函数f(x)的增区间为[得kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$],k∈Z.
(2)∵函数y=g(x-m)=cos(2x-2m)(m>π),
y=f(x)+f(x-$\frac{π}{4}$)=2sin(2x-$\frac{π}{3}$)+1+2sin(2x-$\frac{π}{2}$-$\frac{π}{3}$)+1=2sin(2x-$\frac{π}{3}$)+2-2cos(2x-$\frac{π}{3}$)
=2$\sqrt{2}$sin(2x-$\frac{π}{3}$-$\frac{π}{4}$)+2=2$\sqrt{2}$sin(2x-$\frac{7π}{12}$)+2=-2$\sqrt{2}$cos(2x-$\frac{π}{12}$),
函数y=g(x-m)(m>π)与y=f(x)+f(x-$\frac{π}{4}$)的图象的对称轴完全相同,
故这两个函数的图象最少相差半个周期,即2m=k•$\frac{π}{2}$+$\frac{π}{12}$,k∈Z,即m=k•$\frac{π}{4}$+$\frac{π}{24}$,
故当m>π时,令k=4,可得它的最小值为$\frac{25π}{24}$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,正弦函数的单调性,正弦函数、余弦函数的图象特征,属于中档题.

| A. | 2 | B. | -1 | C. | -1或2 | D. | 1或2 |
 在2017年世乒赛上,中国健儿勇夺冠军,再次掀起同学们对国球的兴趣,某校为了了解学生喜爱打乒乓球是否与性别有关,对高二年级100人进行了问卷调查并根据得到的数据画出如图所示的条形图和扇形图.
在2017年世乒赛上,中国健儿勇夺冠军,再次掀起同学们对国球的兴趣,某校为了了解学生喜爱打乒乓球是否与性别有关,对高二年级100人进行了问卷调查并根据得到的数据画出如图所示的条形图和扇形图.| 喜爱打乒乓球 | 不喜爱打乒乓球 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 | 100 |
(Ⅱ)是否有99.5%的把握认为喜欢打乒乓球与性别有关?说明你的理由,下面的临界值表供参考
| P(K2≥k) | 0.10 | 0.0 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | (-$\frac{π}{4}$,0) | B. | (-$\frac{π}{6}$,0) | C. | ($\frac{π}{3}$,0) | D. | ($\frac{5π}{12}$,0) |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |