题目内容
4. 已知函数f(x)=2|x+1|-|x-2|,x∈[-3,3].
已知函数f(x)=2|x+1|-|x-2|,x∈[-3,3].(Ⅰ)写出函数f(x)的分段解析表达式,并作出f(x)的图象;
(Ⅱ)求不等式|f(x)|>2的解集.
分析 (I)由绝对值的定义和对x分类讨论,可得f(x)的分段函数式,由分段函数的图象画法,可得f(x)的图象;
(II)由f(x)的表达式及图象,求得f(x)=2和f(x)=-2的解,即可得到所求不等式的解集.
解答 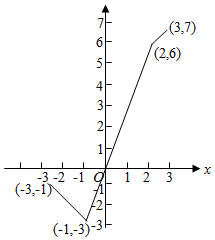 解:(I)由f(x)=2|x+1|-|x-2|,x∈[-3,3].
解:(I)由f(x)=2|x+1|-|x-2|,x∈[-3,3].
可得f(x)=$\left\{\begin{array}{l}{-x-4,-3≤x≤-1}\\{3x,-1<x<2}\\{x+4,2≤x≤3}\end{array}\right.$,
f(x)的图象如图所示
(II)由f(x)的表达式及图象,
当f(x)=2时,可得x=$\frac{2}{3}$;
当f(x)=-2时,可得x=-2或x=-$\frac{2}{3}$;
故f(x)>2的解集为($\frac{2}{3}$,3);f(x)<-2的解集为(-2,-$\frac{2}{3}$);
所以不等式|f(x)|>2的解集为(-2,-$\frac{2}{3}$)∪($\frac{2}{3}$,3).
点评 本题考查分段函数的解析式和图象的画法,考查绝对值不等式的解法,注意结合图象,考查运算能力,属于内计提.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
14. 在2017年世乒赛上,中国健儿勇夺冠军,再次掀起同学们对国球的兴趣,某校为了了解学生喜爱打乒乓球是否与性别有关,对高二年级100人进行了问卷调查并根据得到的数据画出如图所示的条形图和扇形图.
在2017年世乒赛上,中国健儿勇夺冠军,再次掀起同学们对国球的兴趣,某校为了了解学生喜爱打乒乓球是否与性别有关,对高二年级100人进行了问卷调查并根据得到的数据画出如图所示的条形图和扇形图.
(Ⅰ)请将上面的列联表补充完整
(Ⅱ)是否有99.5%的把握认为喜欢打乒乓球与性别有关?说明你的理由,下面的临界值表供参考
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$)
 在2017年世乒赛上,中国健儿勇夺冠军,再次掀起同学们对国球的兴趣,某校为了了解学生喜爱打乒乓球是否与性别有关,对高二年级100人进行了问卷调查并根据得到的数据画出如图所示的条形图和扇形图.
在2017年世乒赛上,中国健儿勇夺冠军,再次掀起同学们对国球的兴趣,某校为了了解学生喜爱打乒乓球是否与性别有关,对高二年级100人进行了问卷调查并根据得到的数据画出如图所示的条形图和扇形图.| 喜爱打乒乓球 | 不喜爱打乒乓球 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 | 100 |
(Ⅱ)是否有99.5%的把握认为喜欢打乒乓球与性别有关?说明你的理由,下面的临界值表供参考
| P(K2≥k) | 0.10 | 0.0 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
15.若实数x,y∈R,则“x>0,y>0”是“x+y>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.以下关于向量说法的四个选项中正确的选项是( )
| A. | 若任意向量$\overrightarrow a与\overrightarrow b$共线且$\overrightarrow a$为非零向量,则有唯一一个实数λ,使得$\overrightarrow a=λ\overrightarrow b$ | |
| B. | 对于任意非零向量$\overrightarrow a与\overrightarrow b$,若$(\overrightarrow a+\overrightarrow b)•(\overrightarrow a-\overrightarrow b)=0$,则$|{\overrightarrow a}|=|{\overrightarrow b}|$ | |
| C. | 任意非零向量$\overrightarrow a与\overrightarrow b$满足$|{\overrightarrow a•\overrightarrow b}|=|{\overrightarrow a}||{\overrightarrow b}|$,则$\overrightarrow a与\overrightarrow b$同向 | |
| D. | 若A,B,C三点满足$\overrightarrow{OA}=\frac{2}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$,则点A是线段BC的三等分点且离C点较近 |
9.下列函数中,在区间(-1,1)上既是奇函数又是增函数的是( )
| A. | y=tanx | B. | y=-x3-3x | C. | y=|sinx| | D. | y=$\frac{1}{x+1}$-1 |
3.《九章算术》中有如下问题:“今有勾八步,股一十五步,问勾中容圆,径几何?”其大意:“已知直角三角形两直角边长分别为8步和15步,问其内切圆的直径为多少步?”现若向此三角形内随机投一粒豆子,则豆子落在其内切圆外的概率是( )
| A. | $\frac{3π}{10}$ | B. | $\frac{3π}{20}$ | C. | $1-\frac{3π}{10}$ | D. | $1-\frac{3π}{20}$ |
 如图,已知四棱锥A-CBB1C1的底面为矩形,D为AC1的中点,AC⊥平面BCC1B1.
如图,已知四棱锥A-CBB1C1的底面为矩形,D为AC1的中点,AC⊥平面BCC1B1.