Question

1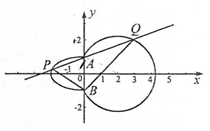．如图，曲线C由左半椭圆M：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0，x≤0）和圆N：（x-2）²+y²=5在y轴右侧的部分连接而成，A，B是M与N的公共点，点P，Q（均异于点A，B）分别是M，N上的动点．
（1）若|PQ|的最大值为4+$\sqrt{5}$，求半椭圆M的方程；
（2）若直线PQ过点A，且$\overrightarrow{AQ}$=-2$\overrightarrow{AP}$，$\overrightarrow{BP}$⊥$\overrightarrow{BQ}$，求半椭圆M的离心率．

Answer 1

分析 （1）A（0，1），B（0，-1），故b=1，|PQ|的最大值为4+$\sqrt{5}$=a+2+$\sqrt{5}$，解得a，即可得出．
（2）设PQ方程：y=kx+1，与圆N的方程联立可得：（k²+1）x²+（2k-4）x=0，解得Q$（\frac{4-2k}{1+{k}^{2}}，\frac{-{k}^{2}+4k+1}{1+{k}^{2}}）$．根据$\overrightarrow{AQ}=-2\overrightarrow{AP}$，可得P$（\frac{k-2}{1+{k}^{2}}，\frac{2{k}^{2}-2k+1}{1+{k}^{2}}）$．由$\overrightarrow{BP}$⊥$\overrightarrow{BQ}$，可得：x_P•x_Q+（y_P+1）•（y_Q+1）=0，把点P，Q的坐标代入可得：解得k，即可得出．

解答 解：（1）A（0，1），B（0，-1），故b=1，|PQ|的最大值为4+$\sqrt{5}$=a+2+$\sqrt{5}$，解得a=2．
∴半椭圆M的方程为：$\frac{{x}^{2}}{4}$+y²=1（-2≤x≤0）．
（2）设PQ方程：y=kx+1，与圆N的方程联立可得：（k²+1）x²+（2k-4）x=0，
x_A+x_Q=$\frac{4-2k}{1+{k}^{2}}$，x_A=0，∴Q$（\frac{4-2k}{1+{k}^{2}}，\frac{-{k}^{2}+4k+1}{1+{k}^{2}}）$．
$\overrightarrow{AQ}=-2\overrightarrow{AP}$，可得（x_Q，y_Q-1）=-2（x_P，y_P-1），故P$（\frac{k-2}{1+{k}^{2}}，\frac{2{k}^{2}-2k+1}{1+{k}^{2}}）$．
$\overrightarrow{BP}$=（x_P，y_P+1），$\overrightarrow{BQ}$=（x_Q，y_Q+1）．由$\overrightarrow{BP}$⊥$\overrightarrow{BQ}$，可得：x_P•x_Q+（y_P+1）•（y_Q+1）=0，
把点P，Q的坐标代入可得：$\frac{k-2}{1+{k}^{2}}$•$\frac{4-2k}{1+{k}^{2}}$+$（\frac{2{k}^{2}-2k+1}{1+{k}^{2}}+1）$•$（\frac{-{k}^{2}+4k+1}{1+{k}^{2}}+1）$=0，
解得k=$\frac{1}{3}$，∴P$（-\frac{3}{2}，\frac{1}{2}）$．
联立直线PQ与作半椭圆M可得：
$（\frac{1}{{a}^{2}}+\frac{1}{9}）$x²+$\frac{2}{3}x$=0，可得x_P=-$\frac{6{a}^{2}}{9+{a}^{2}}$=-$\frac{3}{2}$，解得a=$\sqrt{3}$，
∴e=$\frac{c}{a}$=$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$．

点评 本题考查了椭圆与圆的标准方程及其性质、直线与椭圆及其圆相交弦长问题、向量坐标运算性质、向量垂直与数量积的关系，考查了推理能力与计算能力，属于难题．