题目内容
13.欧拉,瑞士数学家,18世纪数学界最杰出的人物之一,是有史以来最多遗产的数学家,数学史上称十八世纪为“欧拉时代”.1735年,他提出了欧拉公式:eiθ=cosθ+isinθ.被后人称为“最引人注目的数学公式”.若$θ=\frac{2π}{3}$,则复数z=eiθ对应复平面内的点所在的象限为( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由新定义,可得z=eiθ=${e}^{\frac{2π}{3}i}=cos\frac{2π}{3}+sin\frac{2π}{3}$i=$-\frac{1}{2}+\frac{\sqrt{3}}{2}i$,即可复数位置.
解答 解:由题意z=eiθ=${e}^{\frac{2π}{3}i}=cos\frac{2π}{3}+sin\frac{2π}{3}$i=$-\frac{1}{2}+\frac{\sqrt{3}}{2}i$,对应的点为($-\frac{1}{2},\frac{\sqrt{3}}{2}$);
所以在第二象限;
故选:B
点评 本题考查复数的概念和运算,以及三角函数的运算,考查运算能力.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
4.若从2个滨海城市和2个内陆城市中随机选取1个取旅游,那么恰好选1个滨海城市的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
8.为加强对旅游景区的规范化管理,确保旅游业健康持续发展,某市旅游局2016年国庆节期间,在某旅游景点开展了景区服务质量评分问卷调查,调查情况统计如表:
该旅游局规定,将游客的评分分为三个等级,评分在[0,60)的视为差评,在[60,85)的视为中评,在[85,100)的视为好评,现从上述600名游客中,依据游客评价的等级进行分层抽样,选取了6名游客,以备座谈采访之用.
(Ⅰ)若从上述6名游客中,随机选取一名游客进行采访,求该游客的评分不低于60分的概率;
(Ⅱ)若从上述6名游客中,随机选取两名游客进行座谈,求这两名游客的评价全为“好评”的概率.
| 分数分组 | 游客人数 |
| [0,60) | 100 |
| [60,85) | 200 |
| [85,100] | 300 |
| 总计 | 600 |
(Ⅰ)若从上述6名游客中,随机选取一名游客进行采访,求该游客的评分不低于60分的概率;
(Ⅱ)若从上述6名游客中,随机选取两名游客进行座谈,求这两名游客的评价全为“好评”的概率.
18.大学生小王自主创业,在乡下承包了一块耕地种植某种水果,每季投入2万元,根据以往的经验,每季收获的此种水果能全部售完,且水果的市场价格和这块地上的产量具有随机性,互不影响,具体情况如表:
(Ⅰ)设X表示在这块地种植此水果一季的利润,求X的分布列及期望;
(Ⅱ)在销售收入超过5万元的情况下,利润超过5万元的概率.
| 水果产量(kg) | 3000 | 4000 |
| 概率 | 0.4 | 0.6 |
| 水果市场价格(元/kg) | 16 | 20 |
| 概率 | 0.5 | 0.5 |
(Ⅱ)在销售收入超过5万元的情况下,利润超过5万元的概率.
15.甲、乙两家外卖公司,其单个送餐员的日工资方案如下:甲公司底薪70元,每单提成2元;乙公司无底薪,40单以内(含40 单)的部分每单提成4元,超出40 单的部分每单提成6元.假设同一公司的送餐员同一天的送餐单数相同,现从两家公司各抽取一名送餐员,分别记录其100天的送餐单数,得到如下频数分布表:
甲公司被选取送餐员送餐单数频数分布表
乙公司被选取送餐员送餐单数频数分布表
将其频率作为概率,请回答以下问题:
(1)若记乙公司单个送餐员日工资为X元,求X的分布列和数学期望;
(2)小明将要去其中一家公司应聘送餐员,若甲公司承诺根据每位送餐员的表现,每个季度将会增加300元至600元不等的奖金,如果每年按300个工作日计算,请利用所学的统计学知识为他作出选择,去哪一家公司的经济收入可能会多一些?
甲公司被选取送餐员送餐单数频数分布表
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 20 | 40 | 20 | 10 | 10 |
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 10 | 20 | 20 | 40 | 10 |
(1)若记乙公司单个送餐员日工资为X元,求X的分布列和数学期望;
(2)小明将要去其中一家公司应聘送餐员,若甲公司承诺根据每位送餐员的表现,每个季度将会增加300元至600元不等的奖金,如果每年按300个工作日计算,请利用所学的统计学知识为他作出选择,去哪一家公司的经济收入可能会多一些?
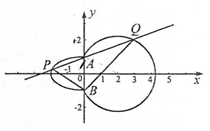 如图,曲线C由左半椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,x≤0)和圆N:(x-2)2+y2=5在y轴右侧的部分连接而成,A,B是M与N的公共点,点P,Q(均异于点A,B)分别是M,N上的动点.
如图,曲线C由左半椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,x≤0)和圆N:(x-2)2+y2=5在y轴右侧的部分连接而成,A,B是M与N的公共点,点P,Q(均异于点A,B)分别是M,N上的动点.