题目内容
如图，正方体ABCD-A1B1C1D1的棱长为1，点M在棱AB上，且AM=| 1 |
| 3 |
| A、圆 | B、抛物线 | C、双曲线 | D、直线 |
考点：圆锥曲线的轨迹问题
专题：圆锥曲线的定义、性质与方程
分析：作PQ⊥AD，作QR⊥D1A1，PR即为点P到直线A1D1的距离，由勾股定理得 PR2-PQ2=RQ2=1，又已知PR2-PM2=1，故PQ=PM，即P到点M的距离等于P到AD的距离．
解答：
解：如图所示：正方体ABCD-A1B1C1D1中，
作PQ⊥AD，Q为垂足，则PQ⊥面ADD1A1，
过点Q作QR⊥D1A1，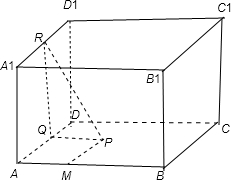
则D1A1⊥面PQR，
PR即为点P到直线A1D1的距离，
由题意可得 PR2-PQ2=RQ2=1．
又已知 PR2-PM2=1，
∴PM=PQ，
即P到点M的距离等于P到AD的距离，
根据抛物线的定义可得，点P的轨迹是抛物线，
故选 B．
作PQ⊥AD，Q为垂足，则PQ⊥面ADD1A1，
过点Q作QR⊥D1A1，
则D1A1⊥面PQR，PR即为点P到直线A1D1的距离，
由题意可得 PR2-PQ2=RQ2=1．
又已知 PR2-PM2=1，
∴PM=PQ，
即P到点M的距离等于P到AD的距离，
根据抛物线的定义可得，点P的轨迹是抛物线，
故选 B．
点评：本题考查抛物线的定义，求点的轨迹方程的方法，体现了数形结合的数学思想，得到PM=PQ是解题的关键．
练习册系列答案
全优点练单元计划系列答案
相关题目
已知如图，四边形ABCD为圆内接四边形，AB是直径，MN切⊙O于C点，∠BCM=38°，那么∠ABC的度数是（ ）| A、38° | B、52° |
| C、68° | D、42° |
已知等比数列{an}，Sn为其前n项和，S3=10，S6=30，则S9=（ ）
| A、50 | B、60 | C、70 | D、90 |
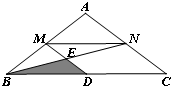如图所示，在△ABC中，AB=AC=10cm，BC=16cm，M、N、D分别是AB、AC、BC的中点，连接DM、BN交于点E，则图中阴影部分△BDE的面积为（ ）| A、4cm2 |
| B、6cm2 |
| C、8cm2 |
| D、12cm2 |