Question

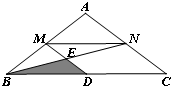如图所示，在△ABC中，AB=AC=10cm，BC=16cm，M、N、D分别是AB、AC、BC的中点，连接DM、BN交于点E，则图中阴影部分△BDE的面积为（　　）

• A、4cm²
• B、6cm²
• C、8cm²
• D、12cm²

Answer 1

考点：相似三角形的性质

专题：计算题

分析：首先过点A作AF⊥BC于F，交MN于K，设EM与DN相交于O，过点O作GH⊥BC于H，交MN于G，首先利用等腰三角形的性质，求得△ABC的高AF的值，然后由题意可得MN是△ABC的中位线，根据中位线的性质，可得MN∥BC，MN=

1

2

BC，继而可判定△OMN∽△OED，根据相似三角形对应高的比等于相似比，即可求得OH的值，然后求得阴影部分的面积．

解答： 解：过点A作AF⊥BC于F，交MN于K，设EM与DN相交于O，过点O作GH⊥BC于H，交MN于G，
∵AB=AC=10，
∴BF=CF=

1

2

BC=

1

2

×16=8（cm），
在Rt△ABF中，AF=

AB2-BF2

=

102-82

=6（cm），
∵M、N分别是AB，AC的中点，
∴MN是中位线，
∴MN∥BC，MN=

1

2

BC=

1

2

×16=8（cm），
∴AK=FK=

1

2

AF=3（cm），
∴NM=DE=8cm，GH⊥MN，
∵MN∥BC，
∴△OMN∽△OED，
∴OG：OH=MN：DE=1，
∴OH=

1

2

GH=

3

2

（cm），
∴S_阴影=

1

2

DE•GH=

1

2

×8×

3

2

=6（cm²）．
故选：B．

点评：此题考查了相似三角形的判定与性质、等腰三角形的性质以及勾股定理等知识．此题难度适中，解题的关键是准确作出辅助线，利用数形结合思想求解．