题目内容
20.单位向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|3$\overrightarrow{a}$-4$\overrightarrow{b}$|=5,则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=( )| A. | 3 | B. | $\sqrt{3}$ | C. | 5 | D. | $\sqrt{5}$ |
分析 由题意知|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,由|3$\overrightarrow{a}$-4$\overrightarrow{b}$|=5可得$\overrightarrow{a}$•$\overrightarrow{b}$=0,从而求得($\overrightarrow{a}$+2$\overrightarrow{b}$)2=${\overrightarrow{a}}^{2}$+4${\overrightarrow{b}}^{2}$+4$\overrightarrow{a}$•$\overrightarrow{b}$=5,从而求得.
解答 解:由题意知,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,
∵|3$\overrightarrow{a}$-4$\overrightarrow{b}$|=5,
∴9${\overrightarrow{a}}^{2}$+16${\overrightarrow{b}}^{2}$-24$\overrightarrow{a}$•$\overrightarrow{b}$=25,
即9+16-24$\overrightarrow{a}$•$\overrightarrow{b}$=25,
故$\overrightarrow{a}$•$\overrightarrow{b}$=0,
故($\overrightarrow{a}$+2$\overrightarrow{b}$)2=${\overrightarrow{a}}^{2}$+4${\overrightarrow{b}}^{2}$+4$\overrightarrow{a}$•$\overrightarrow{b}$=5,
故|$\overrightarrow{a}$+2$\overrightarrow{b}$|=$\sqrt{5}$,
故选:D.
点评 本题考查了平面向量数量积的运算及向量的模的计算,属于中档题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| 产量(kg) | 4000 | 5000 |
| 概率 | 0.5 | 0.5 |
| 苹果的市场价格(元/千克) | 8 | 10 |
| 概率 | 0.4 | 0.6 |
(2)求3年中至少有2年的利润不少于30000元的概率.
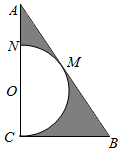 如图所示,△ABC中,∠C=90°,∠B=60°,AB=2$\sqrt{3}$,在三角形内挖去半圆(圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于N),则图中阴影部分绕直线AC旋转一周所得旋转体的内外表面积之比为$\frac{4}{9}$.
如图所示,△ABC中,∠C=90°,∠B=60°,AB=2$\sqrt{3}$,在三角形内挖去半圆(圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于N),则图中阴影部分绕直线AC旋转一周所得旋转体的内外表面积之比为$\frac{4}{9}$.