题目内容
直线xtan
+y+2=0的倾斜角α是（ ）
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
考点：直线的倾斜角
专题：直线与圆
分析：由直线方程求出直线的斜率，再由倾斜角的正切值等于斜率得答案．
解答：
解：∵直线xtan
+y+2=0的斜率为-tan
=-
，
由tanα=-
，且0≤α＜π，得α=
．
故选：C．
| π |
| 3 |
| π |
| 3 |
| 3 |
由tanα=-
| 3 |
| 2π |
| 3 |
故选：C．
点评：本题考查了直线的倾斜角，考查了倾斜角与斜率的关系，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知直线l，m，平面α，β满足l⊥α，m?β，则“l⊥m”是“α∥β”的（ ）
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
当x＞0时，下列函数中最小值为2的是（ ）
A、y=x+
| ||
| B、y=x2-2x+3 | ||
C、y=
| ||
D、y=lnx+
|
若数列{an}是等差数列，则“a1＜a2”是“数列{an}为递增数列”（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、不充分也不必要条件 |
已知tanα=2，则
=（ ）
| cos(π-α) | ||
cos(α-
|
A、-
| ||
| B、-2 | ||
C、
| ||
| D、2 |
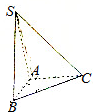如图，在三棱锥S-ABC中，SA⊥底面ABC，AB⊥AC．