题目内容
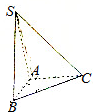 如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥AC.
如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥AC.(1)求证:AB⊥平面SAC;
(2)设SA=AB=AC=1,求点A到平面SBC的距离.
考点:点、线、面间的距离计算,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)根据线面垂直的判定定理证明即可;(2)作出辅助线,求出BC,SD的长,从而求出点到面的距离.
解答:
证明:(1)∵SA⊥底面ABC,∴SA⊥AB,
∵AB⊥AC,∴AB⊥平面SAC;
(2)如图,
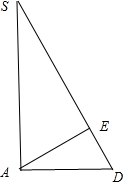
做AD⊥BC,交点为D,连接SD,做AE⊥SD,交点为E,
∵SA⊥底面ABC,∴SA⊥BC,
∵AD⊥BC,∴BC⊥平面SAD,∴BC⊥AE,
∵AE⊥SD,∴AE⊥平面SBC,
∴AE的长度是A到平面SBC的距离,
由勾股定理得BC=
,
(面积相等)AD×BC=AB×AC=1,
∴AD=
,
勾股定理得SD=
,
(面积相等)SA×AD=AE×SD,
即
=AE×
,
∴AE=
,
∴A到平面SBC的距离为
.
∵AB⊥AC,∴AB⊥平面SAC;
(2)如图,

做AD⊥BC,交点为D,连接SD,做AE⊥SD,交点为E,
∵SA⊥底面ABC,∴SA⊥BC,
∵AD⊥BC,∴BC⊥平面SAD,∴BC⊥AE,
∵AE⊥SD,∴AE⊥平面SBC,
∴AE的长度是A到平面SBC的距离,
由勾股定理得BC=
| 2 |
(面积相等)AD×BC=AB×AC=1,
∴AD=
| ||
| 2 |
勾股定理得SD=
| ||
| 2 |
(面积相等)SA×AD=AE×SD,
即
| ||
| 2 |
| ||
| 2 |
∴AE=
| ||
| 3 |
∴A到平面SBC的距离为
| ||
| 3 |
点评:本题考查了线面垂直的判定定理,考查了距离的计算,是一道中档题.

练习册系列答案
相关题目
已知命题p:?x0∈R,sinx0+cosx0=
,命题q:对于实数a,b,a2>b2是a>|b|的必要不充分条件,则( )
| 3 |
| 2 |
| A、“p或q”为假 |
| B、“p或?q”为真 |
| C、“p且q”为真 |
| D、“?p且q”为真 |
某学校在“11•9”举行老师、学生消防知识比赛,报名的学生和教师的人数之比为6:1,学校决定按分层抽样的方法从报名的师生中抽取35人组队进行比赛,已知教师甲被抽到的概率为
,则报名的学生人数是 .
| 1 |
| 10 |
直线xtan
+y+2=0的倾斜角α是( )
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
已知集合M={x∈R|(x+1)(x-2)>0}和N={x∈R|x2+x<0},则集合M是集合N的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知a=(
)
,b=(
)
,c=log
,则a,b,c之间的大小关系为( )
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| A、a>b>c |
| B、c>a>b |
| C、a>c>b |
| D、c>b>a |